Даны координаты вершин пирамиды А1А2А3А4.
Найти:

1. длину ребра А1А2;
2. угол между ребрами А1А2 и А1А4;
3. площадь грани А1А2А3;
4. уравнение плоскости А1А2А3.
5. объём пирамиды А1А2А3А4.

2.10. А1 ( 6; 6; 5), А2 ( 4; 9; 5), А3 ( 4; 6; 11), А4 ( 6; 9; 3).
Решение:

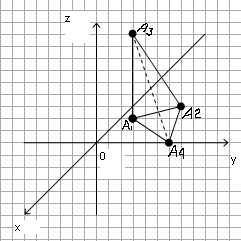
1. Находим длину ребра А1А2

Длина ребра А1А2  равна расстоянию между точками А1 и А2 или модулю вектора . Расстояние между точками А1(x1;y1;z1)  и            А2 (x2;y2;z2) вычисляется по формуле:

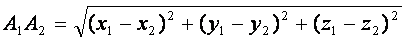
подставим в эту формулу координаты точек и получим:
 единиц
2. Угол между ребрами А1А2 и А1А4 обозначим и вычисляем по формуле:
;
где  = ; = ;
находим координаты векторов, для этого вычитаем из координат конца координаты начала :


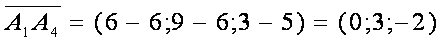
подставляем координаты векторов в формулу и считаем cos?:
;
 (градусов).
3. Площадь грани (треугольника) А1А2А3  находим используя свойства скалярного произведения: площадь параллелограмма, построенного на векторах и численно равна модулю их векторного произведения. Площадь треугольника равна половине площади параллелограмма:

 
Сначала находим координаты векторов:

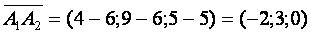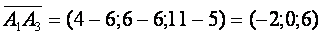
находим их произведение:

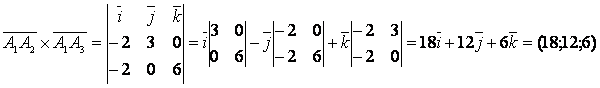
и вычисляем площадь грани:
 кв.единиц

4. Уравнение плоскости A1A2A3 найдем как уравнение плоскости, проходящей через три данные точки A1; A2иA3:

подставим координаты точек A1; A2иA3 .

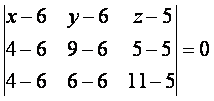
вычислив определитель матрицы получаем уравнение:
  сокращая уравнение на 6 получим уравнение плоскости: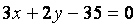 
5. Объем пирамиды A1A2A3A4 равен одной шестой смешанного произведения трех векторов модуль которого числено равен объему праллелепипеда, построенного на этих векторах.
Выразим произведение трех векторов через координаты сомножителей:



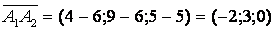
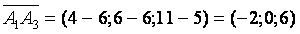
составим из координат векторов и решим матрицу:
 куб.единицы

Ответы:

1. длина ребра А1А2  равна единиц.
2. угол между ребрами А1А2 и А1А4:(градусов).
3. площадь грани А1А2А3  кв.единиц
4. уравнение плоскости А1А2А3:
5. объём пирамиды А1А2А3А4 равен 4 куб.единицы.