|
Провести исследование функции  с указанием с указанием
а) области определения и точек разрыва;
б) экстремумов;
с) асимптот.
По полученным данным построить графики функций.
Решение:
а) Найдем область определения и точки разрыва.
Дана функция  , ,
где  ; ; 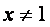
 Функция нечетная. Функция нечетная.
Область определения функции лежит 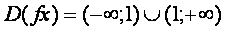
 - точка разрыва функции второго рода, т.к. - точка разрыва функции второго рода, т.к. 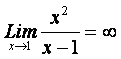
б) Найдем точки экстремумов функции.
Необходимый признак экстремума, если x0 -точка экстремума.
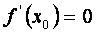
 ; т.к. производная функции в точке экстремума равна нулю (y’=0) , то ; т.к. производная функции в точке экстремума равна нулю (y’=0) , то  , отсюда следует, что , отсюда следует, что
 ; ;  ; ; 
точки экстремумов функции
 

Выпуклость и вогнутость функции.
Определение. Кривая обращена выпуклостью вверх на интервале (а, b), если все ее точки лежат ниже любой ее касательной на этом интервале. Кривая, обращенная выпуклостью вверх, называется выпуклой, а кривая, обращенная выпуклостью вниз – называется вогнутой.
Если во всех точках интервала (a, b) вторая производная функции f(x) отрицательна, то кривая y = f(x) обращена выпуклостью верх (выпукла), а если положительна, то кривая y = f(x) обращена выпуклостью вниз (вогнута).
Найдем вторую производную функции 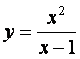
 ; ;
 ; ;
 , ,
 , т.к. , т.к.  , точки перегиба нет. , точки перегиба нет.
Подставим значения экстремумов в производную функции второго поряда, получим при x=0, у’’ = -2 , значит функция в точке  выпукла, при x=2, y”=2, значит функция в точке выпукла, при x=2, y”=2, значит функция в точке  вогнута. вогнута.
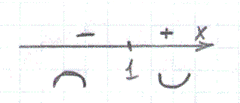
с) Найдем асимптоты функции
вертикальная асимптота проходит через точку разрыва  и и
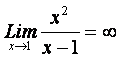
Найдем наклонную асимптоту 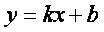
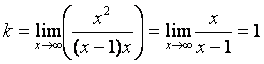
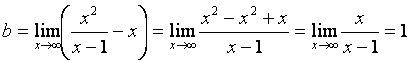
Наклонная асимптота 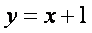
Построим графики функции, проведем асимптоты и покажем точки экстремумов функции

|







