Найти ранг матрицы:
.
Решение

Найдем ранг матрицы методом элементарных преобразований, переходя к эквивалентной треугольной матрице А', из которой сразу можно определить наивысший из порядков отличных от нуля ее миноров, при этом учтем, что:
.
При переходе от данной матрицы А к эквивалентной А' использованы следующие элементарные преобразования:
- умножение строки (столбца) на число, отличное от нуля;
- прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца);
- вычеркивание строки, все элементы которой равны нулю;
- перестановка строк (столбцов) матрицы.

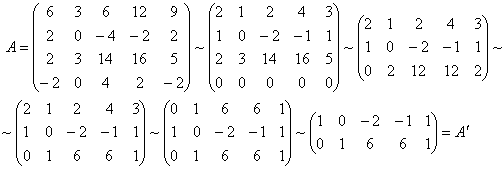
Ранг матрицы А' равен двум, т. к. порядок ее самого большего, отличного от нуля, минора равен двум:
.
Минор большего порядка невозможно сформировать, т. к. матрица А' содержит только две строки.
Вывод: .
Ответ: .