–†–µ—И–µ–љ–Є–µ –Ј–∞–і–∞—З–Є –њ–Њ –≤—Л—Б—И–µ–є –Љ–∞—В–µ–Љ–∞—В–Є–Ї–µ вДЦ76
|
|
–†–µ—И–Є—В—М —Б–Є—Б—В–µ–Љ—Г –ї–Є–љ–µ–є–љ—Л—Е —Г—А–∞–≤–љ–µ–љ–Є–є:
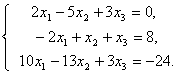
–†–µ—И–µ–љ–Є–µ
–Ш—Б—Б–ї–µ–і—Г–µ–Љ —Б–Є—Б—В–µ–Љ—Г –љ–∞ —Б–Њ–≤–Љ–µ—Б—В–љ–Њ—Б—В—М:
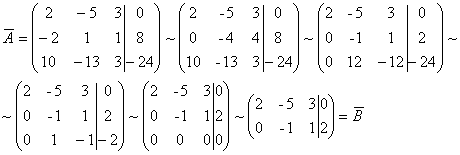
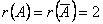
–†–∞–љ–≥–Є –Њ—Б–љ–Њ–≤–љ–Њ–є –Є —А–∞—Б—И–Є—А–µ–љ–љ–Њ–є –Љ–∞—В—А–Є—Ж —Б–Є—Б—В–µ–Љ—Л —Б–Њ–≤–њ–∞–і–∞—О—В, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –і–∞–љ–љ–∞—П —Б–Є—Б—В–µ–Љ–∞ —Б–Њ–≤–Љ–µ—Б—В–љ–∞.
–†–∞–љ–≥ —Б–Є—Б—В–µ–Љ—Л –Љ–µ–љ—М—И–µ —З–Є—Б–ї–∞ –µ–µ –љ–µ–Є–Ј–≤–µ—Б—В–љ—Л—Е (r < n), –Ј–љ–∞—З–Є—В, –і–∞–љ–љ–∞—П —Б–Є—Б—В–µ–Љ–∞ –љ–µ–Њ–њ—А–µ–і–µ–ї–µ–љ–љ–∞—П, —В.–µ. –Є–Љ–µ–µ—В –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ–µ –Љ–љ–Њ–ґ–µ—Б—В–≤–Њ —А–µ—И–µ–љ–Є–є.
–Э–∞–є–і–µ–Љ –≤—Б–µ —А–µ—И–µ–љ–Є—П —Б–Є—Б—В–µ–Љ—Л. –†–µ—И–Є–Љ —Н–Ї–≤–Є–≤–∞–ї–µ–љ—В–љ—Г—О —Б–Є—Б—В–µ–Љ—Г:
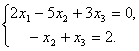
–Т –Ї–∞—З–µ—Б—В–≤–µ –±–∞–Ј–Є—Б–љ–Њ–≥–Њ —А–∞—Б—Б–Љ–Њ—В—А–Є–Љ –Љ–Є–љ–Њ—А:
 . .
–Х–≥–Њ —Н–ї–µ–Љ–µ–љ—В–∞–Љ–Є —П–≤–ї—П—О—В—Б—П –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Л –њ—А–Є –љ–µ–Є–Ј–≤–µ—Б—В–љ—Л—Е —Е1 –Є —Е2. –≠—В–Є –љ–µ–Є–Ј–≤–µ—Б—В–љ—Л–µ –љ–∞–Ј–Њ–≤–µ–Љ –±–∞–Ј–Є—Б–љ—Л–Љ–Є. –Ю—Б—В–∞–≤—И–∞—П—Б—П –љ–µ–Є–Ј–≤–µ—Б—В–љ–∞—П —Е3 вАУ —Б–≤–Њ–±–Њ–і–љ–∞—П. –Х–є –Љ–Њ–ґ–љ–Њ –њ—А–Є–і–∞—В—М –ї—О–±–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ: —Е3 = k, kIR.
–Я–µ—А–µ–љ–µ—Б–µ–Љ —Б–ї–∞–≥–∞–µ–Љ—Л–µ, —Б–Њ–і–µ—А–ґ–∞—Й–Є–µ —Б–≤–Њ–±–Њ–і–љ—Г—О –љ–µ–Є–Ј–≤–µ—Б—В–љ—Г—О, –≤ –њ—А–∞–≤—Л–µ —З–∞—Б—В–Є —Г—А–∞–≤–љ–µ–љ–Є–є —Б–Є—Б—В–µ–Љ—Л, –њ–Њ–ї—Г—З–Є–Љ:
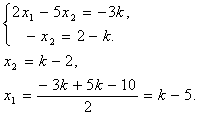
–Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, —А–µ—И–µ–љ–Є–µ –Є—Б—Е–Њ–і–љ–Њ–є —Б–Є—Б—В–µ–Љ—Л –Є–Љ–µ–µ—В –≤–Є–і:  , kIR. , kIR.
–Ю—В–≤–µ—В:  . .
|







