Вычислить предел: .

Решение. I  способ. При  получим, что
   и

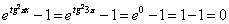
Следовательно, получим неопределенность вида . Сделаем замену переменной. Введем такое t, чтобы , если .

=.

Дальше заменим бесконечно малые в числителе и знаменателе на эквивалентные по формулам (21), (23), (22), (18).
Мы имеем право сделать это в преобразованных выражениях, т.к. для соответствующей функции  выполняется  , если . Получаем:

= .

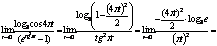
II способ. Поскольку при непосредственном вычислении предела имеем неопределенность типа , то необходимо преобразовать выражение, стоящее под знаком предела. Однако сразу использовать таблицу эквивалентности бесконечно малых нельзя поскольку
, ,         если . Используем свойство периодичности тригонометрических функций, получим
Выражение под знаком предела преобразовано таким образом, что  и , если . Поэтому можно использовать формулы эквивалентности (21), (23), (22), (18). В результате получаем