Дана функция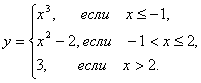
Исследовать ее на непрерывность и разрыв. Построить график.

Решение. На промежутках  заданы аналитические выражения элементарных функций, которые определены и, следовательно, непрерывны на каждом промежутке. Поэтому точками «подозрительными на разрыве», являются точки  и .
Вычислим односторонние пределы функции в точке .
Так как  при , то
.
Так как  при , то
.
Вычислим значение функции в точке :
.
Получим, что выполнены условия непрерывности функции в точке . Поэтому в точке  разрыва функции нет.
Вычислим односторонние пределы функции в точке .
Так как    при    , то
.
Так как    при  , то
.
Получили, что  – точка разрыва I рода (скачка). Значит, функция непрерывна всюду на числовой прямой кроме точки.  в которой она имеет скачок, равный 1.