Решение задачи по высшей математике №41
|
|
Составить уравнение плоскости, проходящей через точки A(1, 0, –1), B(1, 3, –4) и образующей угол  с плоскостью с плоскостью 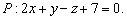
Решение. Не ограничивая общности. Будем искать уравнение плоскости в виде
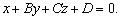
Поскольку точки A(1, 0, –1) и B(1, 3, –4) лежат в искомой плоскости, то их координаты удовлетворяют уравнению этой плоскости. Значит имеем
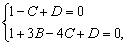
откуда   Подставим найденные значения D и B, выраженные через C, в уравнение плоскости: Подставим найденные значения D и B, выраженные через C, в уравнение плоскости:
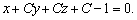
Следовательно, нормальный вектор  . .
Воспользуемся тем, что плоскость образует угол  с плоскостью с плоскостью  нормальный вектор нормальный вектор  которой которой  . По формуле косинуса угла между плоскостями имеем: . По формуле косинуса угла между плоскостями имеем:
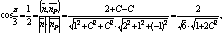
откуда  или или  Находим C, преобразовывая последнее равенство: Находим C, преобразовывая последнее равенство:
   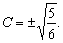
Имеем окончательно уравнение плоскостей:

|







