1. Установить взаимное расположение прямой и плоскости, в случае их пересечения – найти координаты пересечения:
Решение. 1) 1)  и
Определим координаты направляющего вектора прямой  по ее каноническим уравнениям. Это вектор  Нормальный вектор  плоскости  имеет координаты  Найдем скалярное произведение векторов  и : 

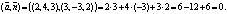
Значит,  и прямая L и плоскость P параллельны. Проверим, не лежит ли прямая L в плоскости P. Для этого определим принадлежность точки  плоскости P, подставив координаты в уравнение плоскости:

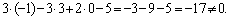
Следовательно,  а значит,
2

 2)  и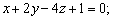
Прямая  имеет направляющий вектор  и точку  Выясним, будет ли  перпендикулярен нормальному вектору  заданной плоскости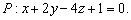

Осталось проверить принадлежность точки  плоскости:

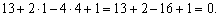
Значит, прямаяL лежит в плоскости P.
3. 3)  и
Направляющий вектор заданной прямой и направляющий вектор  плоскости не коллинеарны и не перпендикулярны, т. к.  и  Значит, . Найдем координаты точки  пересечения прямой и плоскости. Для этого перейдем сначала к параметрическим уравнениям прямой:

Затем в уравнение плоскости P подставим вместо их выражение через параметр t:

Откуда имеем



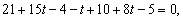
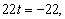
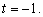
Подставим найденное значение параметра t в параметрические уравнения прямой: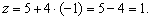   
Итак, .