Решение задачи по высшей математике №35
|
|
Найти координаты точки N, симметричной точке  относительно прямой, проходящей через точки относительно прямой, проходящей через точки  и и  . .
Решение. Для решения задачи воспользуемся следующими рассуждениями: симметричная точке M точка N находится в той же плоскости, что прямая AB и точка M, лежит на перпендикуляре MN к прямой AB и находится от прямойAB на том же расстоянии, что и точка M.
Пусть  Тогда Тогда
1)  – компланарны; – компланарны;
2)  ; ;
3)  ; ;
4) середина отрезка MN лежит на прямой AB.
Составим систему уравнений, используя координатную форму записи условий 1–3.
  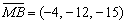
 – компланарны при условии – компланарны при условии  т. е. т. е.  откуда получаем откуда получаем
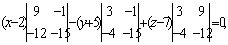
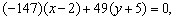
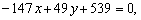
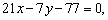
 откуда откуда 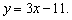
Условие  равносильно условию равносильно условию  или или  что приводит к уравнению что приводит к уравнению
 затем затем
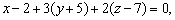
 откуда откуда
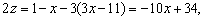
 . .
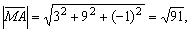
 следовательно, следовательно,
 После подстановки После подстановки  , ,  получим получим  или или  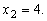
Таким образом, точки  и и  удовлетворяют первым трем условиям. Осталось проверить четвертое. Найдем середины удовлетворяют первым трем условиям. Осталось проверить четвертое. Найдем середины  и и  отрезков отрезков  и и  соответственно и проверим, какая из точек ( соответственно и проверим, какая из точек ( или или  ) лежит на прямой ) лежит на прямой 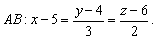
 ли ли 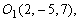
 или или 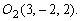
 т. к. т. к.  но но 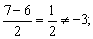
 т. к. т. к. 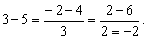
Итак, 
|







