Использовать форму и построить поверхность заданную уравнением

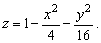
Решение. Используем при исследовании геометрических свойств и форм поверхности метод сечений.
Определим сечение поверхности плоскостями  где  параллельными координатной плоскости Oxy:
 
Очевидно, что это кривые, проекции которых на ось Oxy задаются уравнение
                                                                        (1)
Уравнение (1) при  не имеет решений относительно  Это означает, что соответствующее сечение есть пустое множество точек, а значит, рассматриваемая поверхность целиком расположена ниже плоскости  При  уравнение (1) определяет эллипс

с полуосями  и  вырождающийся в точку (0, 0, 1) при  Заметим, что все эллипсы, получающиеся в сечениях поверхности плоскостями  подобны между собой, причем с уменьшением  их полуоси неограниченно монотонно возрастают.
Дальнейшее уточнение форм можно получить, рассматривая сечения координатными плоскостями Oxz и Oyz:
  и 
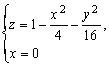
Имеем в первом случае кривую  т. е. параболу с параметром  вершиной в точке   и ветвями, направленными в отрицательную сторону оси Oz. Во втором – параболу  с параметром  вершиной в точке   и аналогичным направлением ветвей.
Выполненное исследование позволяет построить заданную поверхность (рис. 1). Это эллиптический параболоид  с вершиной в точке (0, 0, 1), направленный в сторону убывания значений z с осью симметрии Oz.

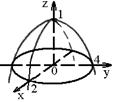
Рис. 1.