Исследовать систему на совместность и найти ее решение:

Решение. Запишем расширенную матрицу системы:

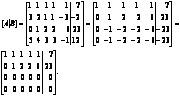
Наибольший порядок отличных от нуля миноров равен 2 (так как любой минор 3-го порядка содержит нулевую строку, а, следовательно, будет равен нулю). Значит,  и          исходная система совместны.
Выберем в качестве базисного минор  Тогда х1, х2 – базисные неизвестные, х3, х4, х5 – свободные. Система,                              равносильная исходной, имеет вид:

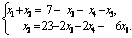
Полагаем х3 = с1, х4 = с2, х5 = с3,
где с1, с2, с3 – произвольные постоянные, и решаем                               указанную систему.
Получаем

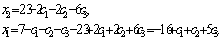
Таким образом получаем множество решений вида