|
Исследовать методами дифференциального исчисления функцию и, используя результаты исследования, построить ее график.
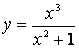
Решение
- Д(у) =R, т.к. х2 +1?0 при любом действительном значении х
- Нули функции:
 х3 =0, х =0. х3 =0, х =0.
- Область определения симметрична относительно начала координат
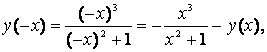 следовательно, функция нечетная, ее график симметричен относительно начала координат. следовательно, функция нечетная, ее график симметричен относительно начала координат.
- Вертикальных асимптот нет.
Наклонные асимптоты имеют вид y = 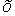 + +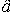 , ,
= 
 , ,
Следовательно у =1*х +0, у =х – наклонная асимптота.
5)

у? =0; х2(х2+3) =0, х2 =0 или х2 +3 =0 нет корней
  х=0 х=0
 у?(х) + + у?(х) + +
  0 х 0 х
Функция возрастает на всей области определения.
Точек экстремума нет.
6)
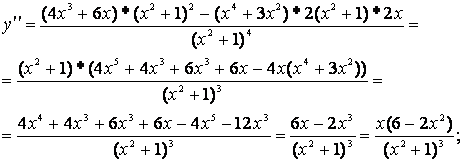
у??(х) =0; х(6-2х2) =0; х1=0 или 6-2х2=0; 2х2=6, х2=3
х2,3=±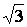
   у??(х) у??(х)
 + - + - + - + -
-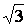 0 0   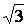 х х
 
вогнутый выгнутый вогнутый выгнутый
Точки (0; 0), 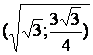 , , 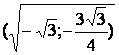 - точка перегиба. - точка перегиба.
7) Дополнительные точки:
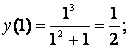 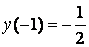
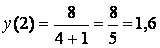 ; у(-2) =-1,6. ; у(-2) =-1,6.
8) Построит график функции:
   у у =х у у =х
2
  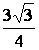
1
 

   -2 - -2 -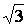 - 1 0 1 - 1 0 1 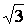 2 х 2 х
 - -
 - -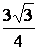
-2
|







