Дана система трех линейных уравнений. Найти решение ее двумя способами: методом Крамера и методом Гаусса.
1.10.

Решение:
x; y; z; - неизвестные
31; 20; 9 – свободные члены системы
Составим матрицу системы уравнений из коэффициентов при неизвестных :

Найдем определитель матрицы по формуле:
(a11a22a33 + a12a23a31 + a13a21a32) – (a13a22a31 + a12a21a33 + a11a23a32)

Определитель системы не равен нулю, поэтому система совместна
и определена и имеет единственное решение.
Решение системы методом Крамера.
  , где
Ai – определитель матрицы, с  замененным i-тым столбцом свободными членами.
Запишем формулы для нахождения каждого неизвестного:
  
Вычислим определитель матрицы с замененным 1 столбцом на свободные члены системы уравнений:
Вычислим определитель матрицы с замененным 2 столбцом на свободные члены системы уравнений:

Вычислим определитель матрицы с замененным 3 столбцом на свободные члены системы уравнений:

 ;   ; 

Решение системы уравнений методом Гаусса:

К матрице        
добавим столбец свободных членов 

Полученная матрица называется расширенной матрицей системы:

Метод Гаусса (метод исключения неизвестных) состоит в том, что расширенную матрицу системы с помощью элементарных преобразований мы приводим к треугольному виду. Треугольной называется матрица у которой ниже главной диагонали находятся нули. Для этого находим коэффициенты k2 - для второй и    k3 – для третьей строк такие, чтобы при сложении  первой строки, умноженной на такой коэффициент и соответствующей ему строки, в первом столбце этой строки получился «0».
Определяем коэффициены для строк:
k2=-5 и k3=-3
и делаем преобразование матрицы:

~
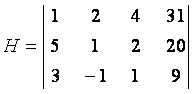так как во втором столбце третьей строки находится не 0, мы делаем еще одно преобразование для третьей строки. Определяем коэффициент для получения нуля во втором столбце третьей строки после умножения второй строки и для сложения с третьей строкой. Коэффициент будет равен:

После преобразования получаем треугольную матрицу с нулями под главной диагональю:

Преобразуем матрицу в систему уравнений:

Решаем систему уравнений начиная с нижнего,
Вычисленные значения переменных подставляем для решения в верхние уравнения и находим.

z=7;  y = 1;  x=1

Полученный результат совпадает с результатом, полученным при решении методом Крамера.
Проверим правильность решения методом подстановки неизвестных в уравнения системы:
1)
2)
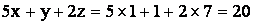
3)
полученные ответы совпадают со свободными членами исходной системы.
Вывод: значения неизвестных найдены правильно.

Ответ:x=1; y = 1; z=7