Решение задачи по высшей математике №64
|
|
Исследовать функцию  и построить ее график. и построить ее график.
Решение. Исследование функции произведем согласно указанному выше плану.
1. Область определения функции:

2. Область значений E(f) укажем по результатам исследования.
3. Исследуем функцию на четность и нечетность.

Функция не является четной и нечетной.
4. Функция непериодическая.
5. Найдем точки пересечения графика с координатными осями.
Если у = 0, т. е.  то х = 1, х = –3 – точки пересечения оси Ох (нули функции). то х = 1, х = –3 – точки пересечения оси Ох (нули функции).
Если х = 0, то у = 3 – точка пересечения оси Оу.
6. Найдем промежутки знакопостоянства функции. Используем метод интервалов (рис. 6).

Рис. 6.
Получаем:  если если   если если 
7. Функция непрерывна на всей числовой оси.
8. Асимптот нет.
9. Исследуем функцию на монотонность и экстремум. Найдем 

Производная существует  Критическими точками являются те, для которых Критическими точками являются те, для которых  т. е. т. е.  и и 
Исследуем знак производной для конкретных промежутков, на которые критические точки делят числовую ось (рис. 7).

Рис. 7
Согласно теореме 1, функция возрастает на множестве  и убывает на и убывает на  что схематически показано на рис. 7. В точке что схематически показано на рис. 7. В точке  она имеет локальный максимум, а в точке х = 1 – минимум. Найдем их значения: она имеет локальный максимум, а в точке х = 1 – минимум. Найдем их значения:


10. Исследуем график функции на выпуклость, вогнутость и перегиб. Вычислим производную 2-го порядка:
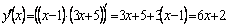
Если  то то  т. е. т. е.  – критическая точка 2-го рода, иных нет. – критическая точка 2-го рода, иных нет.
Имеем  если если  и и  если если  (рис. 8). (рис. 8).

Рис. 8
Значит, график функции является выпуклым на  и вогнутым на и вогнутым на  согласно теореме 6. согласно теореме 6.  – точка перегиба (теорема 7). – точка перегиба (теорема 7).
11. Используя полученные данные, построим график функции (рис. 9).

Рис. 9
Заметим, что 
|







