|
Найти уравнение касательной к параболе y = ax +bx +bx +cx+d параллельной прямой Ax+By+C = 0. Сделать чертеж. +cx+d параллельной прямой Ax+By+C = 0. Сделать чертеж.
a |
b |
c |
d |
A |
B |
C |
1/3 |
2 |
– 1/2 |
2/3 |
1 |
–1 |
1 |
y =  x x +2x +2x – –  x + x + ; x – y +1 = 0 ; x – y +1 = 0
уравнение касательной y = f(x) +f (x (x )(x – x )(x – x ) )
K = K = K
K = y = y = x = x +4x – +4x – 
y = x+1
K = y = y = 1 = 1
x +4x – +4x –  = 1 = 1
x +4x – +4x – 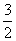 = 0 = 0
D = 16 +6 = 22
x = =  ; x ; x =0,35; x =0,35; x = –4,35 = –4,35
f(x ) = f(0,35) = ) = f(0,35) =  (0,35) (0,35) +2(0,35) +2(0,35) – –  0,35+ 0,35+  0,75 0,75
f(x ) = f(–4,35) = ) = f(–4,35) =  (–4,35) (–4,35) +2(–4,35) +2(–4,35) – – 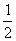 (–4,35)+ (–4,35)+  13,25 13,25
A(0,35;0,75) B(–4,35;13,25)
Первая касательная
y = 0,75x+(x – 0,35)
y = 0,4+x
Вторая касательная
y = 13,25+(x+4,35)
y = 17,6+x
D(y) = R
f(–x) =  (– x) (– x) +2(– x) +2(– x) – –  (– x)+ (– x)+   f(x) f(x)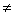 –f(x) –f(x)
y = x = x +4x – +4x – 
y = 0 = 0
x +4x – +4x –  = 0 = 0
D = 16+2 = 18
x = = 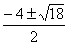 ; x ; x =0,12; x =0,12; x = –4,12 = –4,12
x |
(–  ; – 4,12) ; – 4,12) |
– 4,12 |
(– 4,12;0,12) |
0,12 |
(0,12; +  ) ) |
y |
+ |
0 |
– |
0 |
+ |
y |

|
13,36 |

|
0,64 |

|
f(–4,12) 13,36; f(0,12) 13,36; f(0,12) 0,64 0,64
y = 2x+4 = 2x+4
y = 0 = 0
2x+4 = 0
x = – 2
x |
(–  ; – 2) ; – 2) |
– 2 |
(–2; +  ) ) |
y |
– |
0 |
+ |
y |

|
7 |

|
f(–2) = 7
Пересечение с осями:
с OY y = 
y = x +1 y = x+0,4 y =17,6+x
|







