привести уравнение к каноническому виду и определить тип поверхности, которую оно задает:
1)
2)
3)
4)
Решение. Воспользуемся методом выделения полных квадратов.
1) Преобразуем левую часть уравнения:




Значит, уравнение равносильно
 или

Имеем уравнение однополосного гиперболоида, центр которого находится в точке (–1, 1, 2) и ось, прямая, параллельная оси Oz и проходящая через точку (–1, 1, 2).
2) Так как


то заданное уравнение равносильно уравнению
 или  что приводит окончательно к уравнению гиперболического параболоида  следовательно в точку (-1, 0, 1).

3)

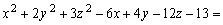
Поэтому имеем
 или

Это уравнение эллипсоида с центром в точке (3, – 1, 2).
4)  приводится к уравнению



Это уравнение эллиптического цилиндра смещенного в точку (– 2, 5, 0).