|
Исследовать функцию и построить ее график
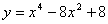 . .
Решение. 1. Область определения функции: х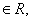 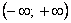 . .
2. Функция является четной, потому что сочетает четные степени аргумента х.
3. Найдем пересечения графика с осями координат:
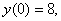 т.е. график пересекает ось Y в точке (0; 8). т.е. график пересекает ось Y в точке (0; 8).
Приравняем у к нулю и решим уравнение:
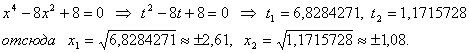
Следовательно, ось Х график пересекает в четырех точках (-2,61; 0), (-1,08; 0), (2,61; 0), (1,08; 0).
4. Возьмем первую производную и найдем точки подозрительные на экстремум:
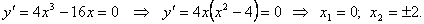
Рассмотрим поведение первой производной в окрестности этих трех точек. Вычислим значения производной в точках -1, 0, 1, 4, 5 и занесем данные в таблицу.
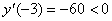
|
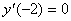
|
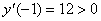
|
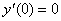
|
убывает |
min |
возрастает |
max |
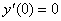
|
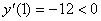
|
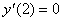
|
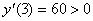
|
max |
убывает |
min |
возрастает |
Покажем поведение первой производной на рисунке, представляющем числовую ось:
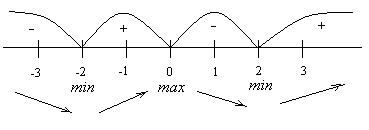
5. Найдем интервалы выпуклости, вогнутости и точки перегиба, для этого возьмем вторую производную и приравняем ее к нулю:
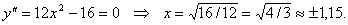
Рассмотрим знак второй производной в окрестности точек 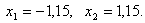
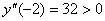 |
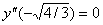
|
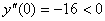
|
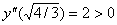
|
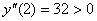
|
вогнутый |
т. перегиба |
выпуклый |
т. перегиба |
вогнутый |
Покажем поведение второй производной на числовой оси:
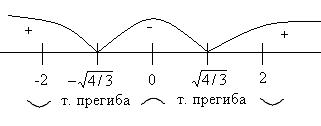
6. Вычислим координаты точек максимума, минимума и точек перегиба.
Точка минимума: x = -2, 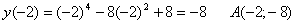
Точка перегиба: x = -1,15, 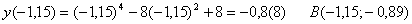
Точка максимума: x = 0, 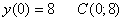
Точка перегиба: x = 1,15, 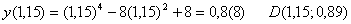
Точка минимума: x = 2, 
Дополним данными о точках пересечения с осью Х: (-2,61; 0), (-1,08; 0), (2,61; 0), (1,08; 0).
Учтем, что график симметричен относительно оси Y.
Полученных данных достаточно для построения графика функции 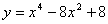 : :
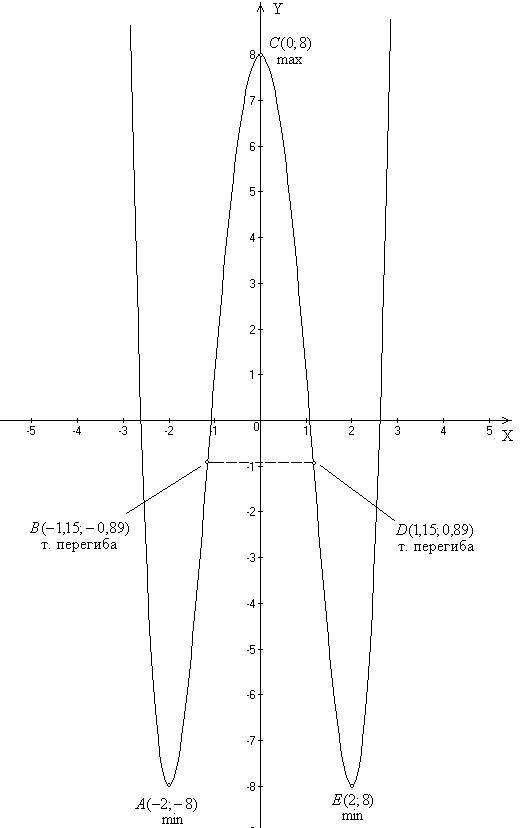
|







