Найти особые точки следующей системы. Определить её тип. Построить схематически фазовые траектории в окрестности каждой особой точки.
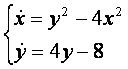
Решение.
1) Находим точки покоя:
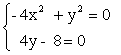 ? ? 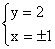 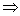 2 две особые точки: 2 две особые точки: 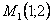 , , 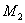 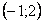
2) Найдем якобиан системы:
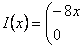 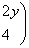
3) Возьмем точку 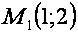 : :
Якобиан в этой точке равен:
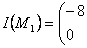 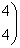
Найдем собственные значения, посчитав следующий определитель:
¦I-?E¦=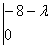 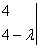 = = 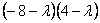 = 0, отсюда = 0, отсюда
l1 = 4 , l2 = - 8 , так как собственные значения l1 , l2 разных знаков, то
Найдем собственные вектора, соответствующие найденным собственным значениям:
Для 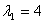 : ¦I-4E¦= : ¦I-4E¦= 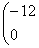 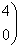 ? ? 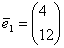 ~ ~ 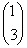
Для 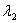 = -8 : ¦I-(-8)E¦= = -8 : ¦I-(-8)E¦= 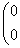 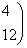 ? ? 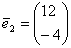 ~ ~ 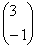
Построим фазовые траектории в окрестности точки 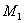 . .
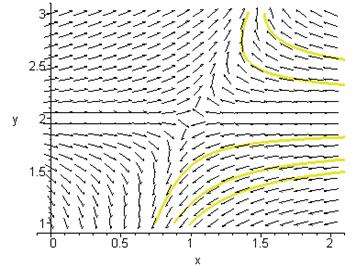
4) Теперь рассмотрим точку 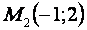 : :
Якобиан в этой точке равен:
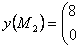 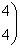
Найдем собственные значения:
¦I-?E¦=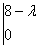 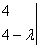 = = 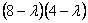 = 0 ? l3 = 4 l4 = 8 , так как собственные значения l1 , l2 одного знаков, то = 0 ? l3 = 4 l4 = 8 , так как собственные значения l1 , l2 одного знаков, то
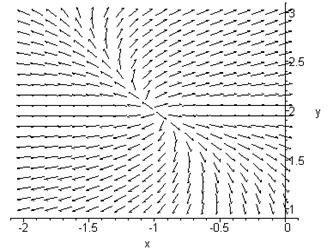
? эта точка типа неустойчивый узел.
Найдем собственные вектора, соответствующие найденным собственным значениям:
Для 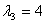 : ¦I-4E¦= : ¦I-4E¦= 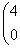 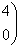 ? ? 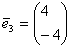 ~ ~ 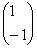
Для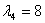 : ¦I-8E¦= : ¦I-8E¦= 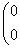 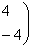 ? ? 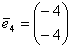 ~ ~ 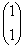
Построим фазовые траектории в окрестности точки 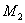 : :
|







