Используя формулу Пуанкаре-Бендиксона, доказать существование цикла у уравнения или системы.
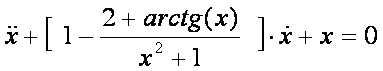
Решение.
1) Составим систему:
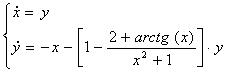 
2) Составим матрицу системы:
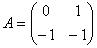
Найдем собственные значения, посчитав следующий определитель:
 , , 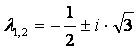
Вещественная часть собственных значений равна:
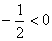 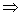 полином гурвицев . полином гурвицев .
3) Используем теорему о том, что если в уравнении
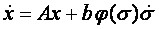 , А – это гурвицева матрица и , А – это гурвицева матрица и
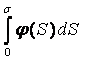 - ограниченная - ограниченная 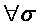 , ,
то система диссипативна.
Поэтому сделаем замену: 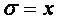 , , 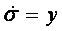
и докажем ограниченность 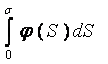
Посчитаем интеграл:
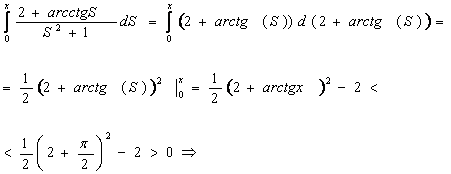
 интеграл ограничен, т. е. является сходящимся. интеграл ограничен, т. е. является сходящимся.
 Система диссипативна. Система диссипативна.
4) Убедимся, что (0, 0) - единственное состояние равновесия:
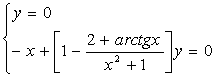 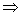 
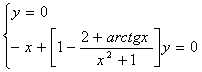 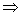
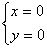
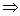 других состояний равновесия нет. других состояний равновесия нет.
5) Докажем, что матрица Якоби антигурвицева.
Якобиан нулевого решения:
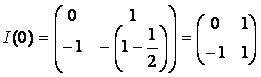
Найдем собственные значения, посчитав следующий определитель:
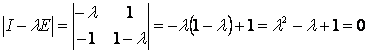 , ,
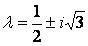 , ,
Вещественная часть собственных значений равна:
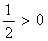 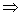 полином антигурвицев полином антигурвицев
(т.е. (0,0) – неустойчивое состояние равновесия).
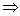 Т. к. матрица Якоби – антигурвицева и система диссипативна, то по соответствующей теореме у исходного уравнения существует цикл. Т. к. матрица Якоби – антигурвицева и система диссипативна, то по соответствующей теореме у исходного уравнения существует цикл.
|







