Методом Пуанкаре найти приближенно периодические решения данных уравнений.
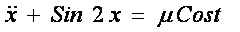 , ,
Решение.
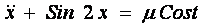 , где , где
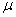 - малый параметр. - малый параметр.
В окрестности x = 0 функцию sin(2x) можно разложить в ряд Тейлора и взять первые 2 члена ряда (остальными можно пренебречь в силу их малости) :
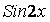 ~ ~ 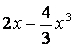 , тогда исходное уравнение перепишем в виде: , тогда исходное уравнение перепишем в виде:

 Сделаем замену: Сделаем замену:
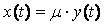 , , 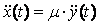 , тогда , тогда
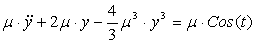 , ,
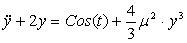 , заменим , заменим
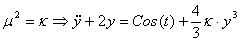 (*) (*)
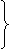 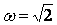 - не является целым числом и - не является целым числом и
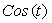 - 2 - 2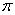 - периодическая функция - периодическая функция 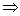
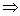 исходное уравнение всегда имеет 2 исходное уравнение всегда имеет 2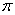 - периодическое решение. - периодическое решение.
Решение будем искать в виде ряда по степеням малого параметра, то есть в виде
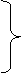 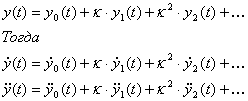 подставим ряды в уравнение (*) подставим ряды в уравнение (*) 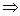

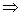  
Приравняем коэффициенты при одинаковых степенях параметра 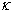 в левой и правой частях последнего равенства: в левой и правой частях последнего равенства:
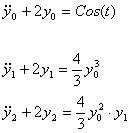 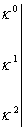
…………………………………
Поскольку 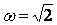 , порождающее уравнение имеет единственное периодическое решение, которое будем искать в виде: , порождающее уравнение имеет единственное периодическое решение, которое будем искать в виде:
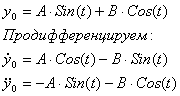
И подставим в уравнение (*):
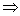 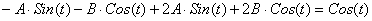

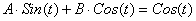 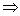 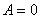 , ,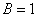 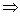 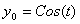

Далее:
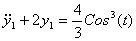 , , 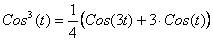
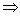
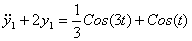  (**) (**)
Аналогично рассчитаем:
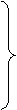 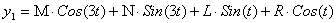
подставим
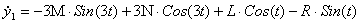 в в
уравнение (**)
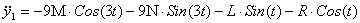

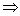
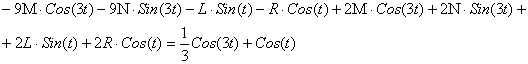
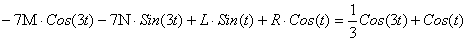
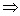 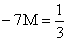
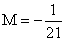 , , 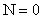 , , 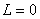 , , 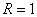 . .
   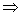 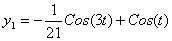

Подставим найденные функции x0 и x1 в правую часть уравнения
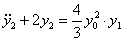 , тогда оно примет вид: , тогда оно примет вид:
 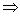 
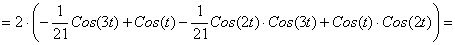
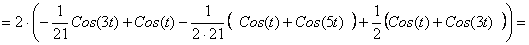
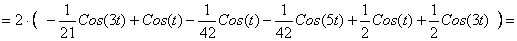
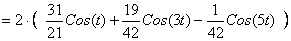

Будем искать решение последнего уравнения в виде:
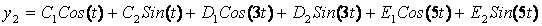
Найдем:
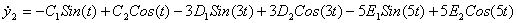
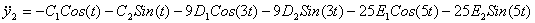
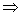

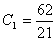 ; ; 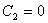 ; ;
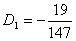 ; ; 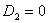 ; ;
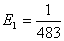 ; ; 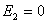
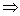
 
 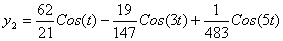
Итак, справедливо приближенное равенство:
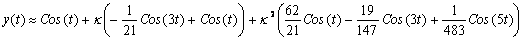
Сделаем обратную замену, чтобы вернуться к x(t):
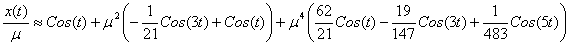

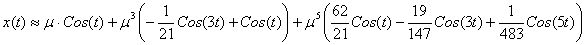 (***) (***)

Используя пакет Mathcad, сравним полученное решение (***) с точным решением исходного уравнения на периоде [0, 2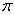 ]. Для этого найдем для решения (***) значения x(0) и ]. Для этого найдем для решения (***) значения x(0) и 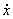 (0), после чего найдем решение исходного уравнения с заданными начальными условиями, например, методом Рунге-Кутта. Результаты расчетов приведены ниже. (0), после чего найдем решение исходного уравнения с заданными начальными условиями, например, методом Рунге-Кутта. Результаты расчетов приведены ниже.
Исследуемое уравнение: 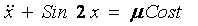 , ,
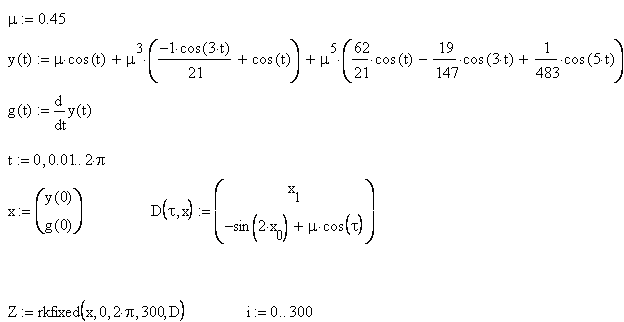
График для µ=0.45 (жирная линия – решение методом Рунге-Кутта)
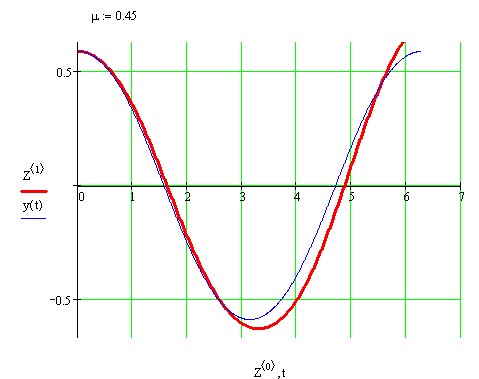
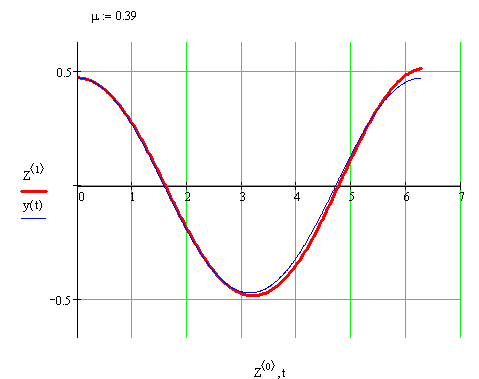
График для µ=0.39 (жирная линия – решение методом Рунге-Кутта)
|







