|
Дана задача линейного программирования 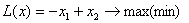 при ограничениях при ограничениях 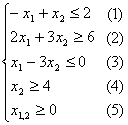 . .
Графическим методом найти оптимальные решения при стремлении целевой функции к максимальному и минимальному значениям.
Решение:
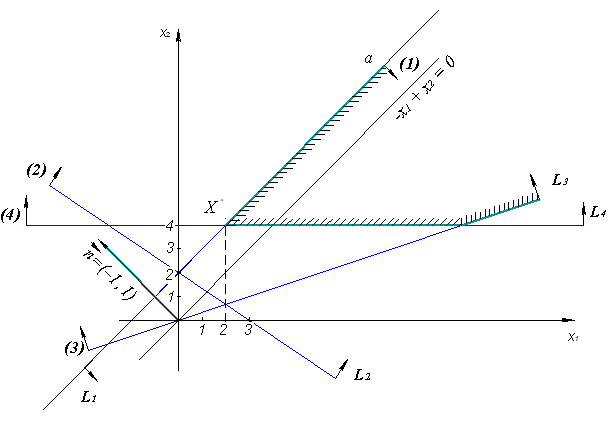
Строим область допустимых решений задачи. Нумеруем ограничения задачи. В прямоугольной декартовой системе координат (см. рис.) строим прямую 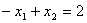 ( (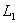 ), соответствующую ограничению (1). Находим, какая из двух полуплоскостей, на которые эта прямая делит всю координатную плоскость, является областью решений неравенства (1). Для этого достаточно координаты какой-либо точки, не лежащей на прямой, подставить в неравенство. Так как прямая ), соответствующую ограничению (1). Находим, какая из двух полуплоскостей, на которые эта прямая делит всю координатную плоскость, является областью решений неравенства (1). Для этого достаточно координаты какой-либо точки, не лежащей на прямой, подставить в неравенство. Так как прямая 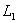 не проходит через начало координат, подставляем координаты точки О (0, 0) в первое ограничение 0 + 0 ? 2. Получаем неравенство 0 ? 2. Следовательно, точка О лежит в полуплоскости решений. Таким образом, стрелки на концах прямой не проходит через начало координат, подставляем координаты точки О (0, 0) в первое ограничение 0 + 0 ? 2. Получаем неравенство 0 ? 2. Следовательно, точка О лежит в полуплоскости решений. Таким образом, стрелки на концах прямой 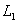 должны быть направлены в полуплоскость, содержащую точку О. Аналогично строим прямые должны быть направлены в полуплоскость, содержащую точку О. Аналогично строим прямые 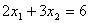 ( (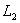 ), ), 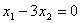 ( (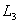 ), ), 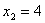 ( (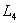 ), и области решений ограничений (2), (3) и (4). Находим общую часть полуплоскостей решений, учитывая при этом условия неотрицательности; полученную область допустимых решений отметим (см. рис.) штриховкой. ), и области решений ограничений (2), (3) и (4). Находим общую часть полуплоскостей решений, учитывая при этом условия неотрицательности; полученную область допустимых решений отметим (см. рис.) штриховкой.
Строим нормаль линий уровня 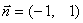 и одну из этих линий, например, и одну из этих линий, например, 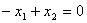 . Для отыскание максимума целевой функции линию уровня перемещаем в направлении нормали до опорной прямой. Эта прямая проходит через луч . Для отыскание максимума целевой функции линию уровня перемещаем в направлении нормали до опорной прямой. Эта прямая проходит через луч 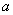 , принадлежащий прямой, ограничивающей область допустимых решений и соответствующей неравенству (1) с вершиной в т.Х* пересечения прямых, ограничивающих область допустимых решений и соответствующих неравенствам (1) и (4). Определяем координаты точки , принадлежащий прямой, ограничивающей область допустимых решений и соответствующей неравенству (1) с вершиной в т.Х* пересечения прямых, ограничивающих область допустимых решений и соответствующих неравенствам (1) и (4). Определяем координаты точки 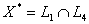 . .
Решая систему 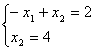 получаем получаем 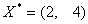 . Вычисляем . Вычисляем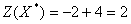 . .
 Следовательно, данная линейная форма достигает максимума в точках, принадлежащих лучу Следовательно, данная линейная форма достигает максимума в точках, принадлежащих лучу 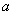 и это максимальное значение линейной формы равно 2. и это максимальное значение линейной формы равно 2.
Минимальное же значение данной линейной формы не ограничено.
Ответ: 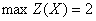 при при 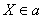 , в частности при , в частности при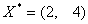 . .
|







