Решение задачи по высшей математике №470
|
- Дано квадратне рівняння
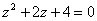 . .
а) знайдіть корені z1 і z2 рівняння.
Розв‘язання.
Знаходимо дискримінант:
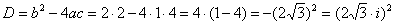
Знаходимо корені z1 і z2 рівняння:
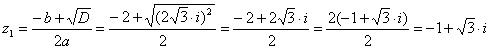
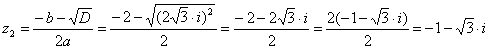
б) знайдіть модуль r та аргумент ? комплексних чисел z1 і z2
Розв‘язання.
Модуль комплексного числа розраховується за формулою: 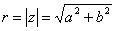
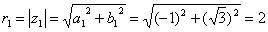
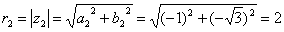
Кут ? між додатним напрямком осі Ох і відрізком ОР є аргументом комплексного числа z. Аргумент обчислюється за формулами:
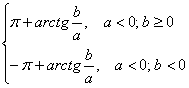 
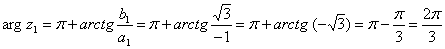
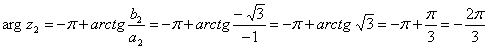
в) запишіть комплексних чисел z1 і z2 в алгебраїчній та тригонометричній формах.
Розв‘язання.
Алгебраїчна форма:
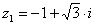
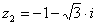
Тригонометрична форма
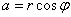 , , 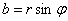 , тому , тому 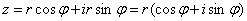
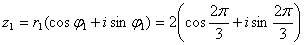
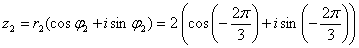
г) піднесіть z1 до шостого ступеня
Розв‘язання.
Піднесення комплексного числа до шостого ступеня виконується за формулою Мавра:
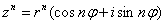
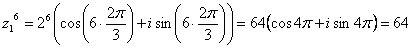
д) добудьте корінь другого ступеня із комплексного числа z2
Розв‘язання.
Корінь n-го ступеня з комплексного значення має n різних значень, які знаходяться за формулою:
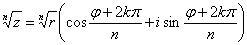 , де k=0,1,2…(n-1) , де k=0,1,2…(n-1)
Знайдемо два значення 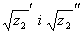 комплексного числа, узявши k=0, k=1. комплексного числа, узявши k=0, k=1.
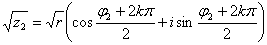
Якщо k=0, то
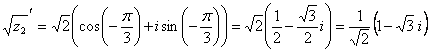
Якщо k=1, то
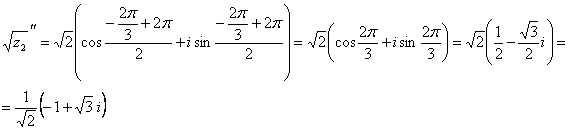
|







