|
Установить совместность системы уравнений и решить
а) 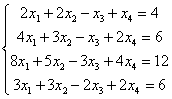 б) б) 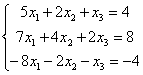 . .
Решение:
а) Запишем матрицу коэффициентов системы А и расширенную матрицу системы В: 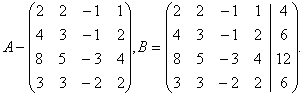
Вертикальной чертой мы отделили элементы матрицы системы (матрица А) от свободных членов системы. Определим ранги матрицы А и В.
Для этого проведём преобразования матрицы В:
- Умножим на 2 элементы второй строки;
От четвертой строки, умноженной на 2 отнимем первую строку, умноженную на 3.
- От второй строки отнимем третью
От третьей строки отнимем первую строку, умноженную на 4
- К третьей строке добавим вторую, умноженную на 3
- Третью строку разделим на 4
Прибавим к четвёртой строке третью строку
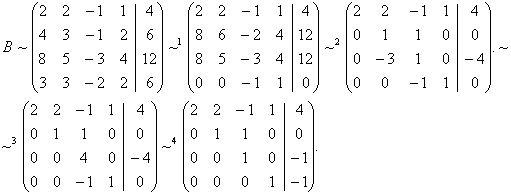
Отсюда следует, что r(В)?4, но минор четвертого порядка матрицы А
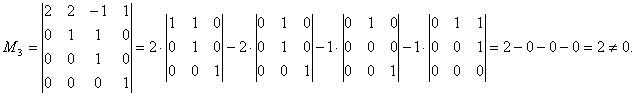
Следовательно, r(B) = r(A) = 4, т.е. данная система совместна.
Но последняя матрица 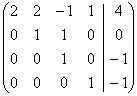 - это расширенная матрица - это расширенная матрица
системы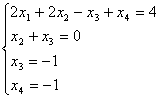
"Обратным ходом" метода Гаусса из последнего уравнения системы находим х4 = – 1; из предпоследнего х3 = – 1; из второго х2 = – х3 = 1; из первого х1 = (4 – х4 + х3 – 2 х2) / 2 = (4 + 1 – 1 – 2 / 2 = 1.
Ответ: 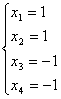
б) Подсчитаем ранги матрицы системы А и расширенной матрицы В.
Имеем: 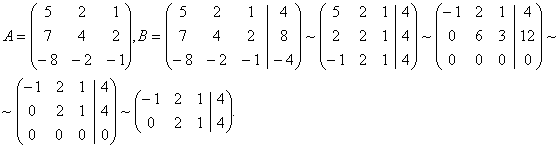
Минор 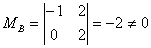 , r(В)=r(A)=2, т.е. данная система совместна. Исходная система равносильна следующей системе: , r(В)=r(A)=2, т.е. данная система совместна. Исходная система равносильна следующей системе: 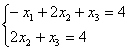
Тогда 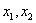 - базисные неизвестные, - базисные неизвестные, 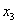 - свободное неизвестное. Перенесем слагаемые с - свободное неизвестное. Перенесем слагаемые с 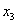 в правую часть уравнения: в правую часть уравнения:
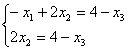
Тогда 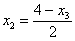 , а по формулам Крамера: , а по формулам Крамера:
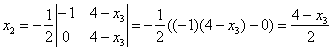
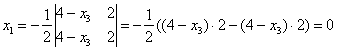
Полагая 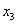 = с (с = с (с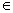 R), получаем: R), получаем: 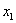 = 0; = 0; 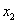 = = 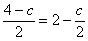 , т.е. исходная система имеет бесконечное множество решений: [0 , т.е. исходная система имеет бесконечное множество решений: [0 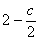 c], с c], с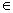 R. R.
Ответ: 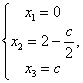 с с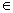 R. R.
|







