- . Даны четыре вектора
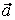 (а1, а2, а3), (а1, а2, а3), 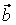 (b1, b2, b3), (b1, b2, b3),
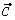 (c1, c2, c3) и (c1, c2, c3) и 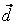 (d1, d2, d3) в некотором базисе. Показать, что векторы (d1, d2, d3) в некотором базисе. Показать, что векторы 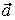 , , 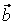 , , 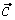 образуют базис, и найти координаты вектора образуют базис, и найти координаты вектора 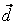 в этом базисе. в этом базисе.
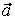 (1,3,5), (1,3,5), 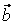 (0,2,0), (0,2,0), 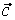 (5,7,9), (5,7,9), 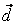 (0,4,16). (0,4,16).
Решение: Как известно, базисом в пространстве 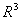 является любая упорядоченная система из трёх линейно независимых векторов. Покажем, что векторы является любая упорядоченная система из трёх линейно независимых векторов. Покажем, что векторы 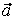 , , 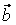 и и 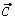 линейно независимы, т.е. выполняется равенство: линейно независимы, т.е. выполняется равенство:
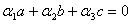
при условии, что все числа 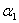 , , 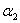 , , 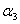 одновременно равны нулю. Подставляя в это равенство координаты векторов одновременно равны нулю. Подставляя в это равенство координаты векторов 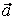 , , 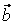 , , 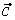 , получаем: , получаем:
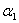 (е1 + 3е2 + 5е3) + (е1 + 3е2 + 5е3) + 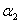 (2е2) + (2е2) + 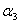 (5е1 + 7е2 + 9е3) = 0 (5е1 + 7е2 + 9е3) = 0
или (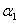 + 5 + 5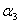 ) • е1 + (3 ) • е1 + (3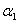 + + 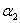 + 7 + 7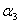 ) • е2 +(5 ) • е2 +(5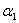 + 9 + 9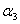 ) • е3 = 0 ) • е3 = 0
Для того, чтобы вектор, разложенный по базису е1, е2, е3 был равен нулевому вектору, его координаты должны равняться нулю, т.е.
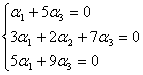
Получим однородную систему трех линейных уравнений с тремя неизвестными 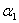 , , 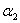 , , 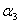 . Такая система имеет нулевое решение ( . Такая система имеет нулевое решение (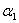 =0, =0, 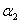 =0, =0, 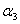 =0), если её определитель не равен нулю. =0), если её определитель не равен нулю.
Поскольку 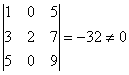 , ,
то векторы 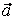 , , 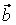 , , 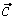 линейно независимы. Следовательно, они образуют базис и вектор линейно независимы. Следовательно, они образуют базис и вектор 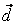 является линейной комбинацией векторов является линейной комбинацией векторов 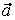 , , 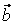 , , 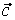 : : 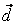 = =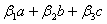 . Числа . Числа 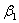 , , 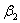 , , 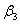 будут координатами вектора будут координатами вектора 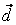 в базисе в базисе 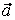 , , 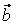 , , 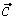 . Найдем их. . Найдем их.
Воспользовавшись разложением 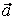 , , 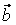 , , 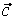 , , 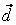 в базисе е1, е2, е3, имеем: в базисе е1, е2, е3, имеем:
4 е2 + 16 е3 = 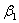 ( е1 + 3 е2 + 5 е3) + ( е1 + 3 е2 + 5 е3) + 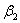 (2 е2) + (2 е2) + 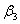 (5 е1 + 7 е2 + 9 е3) (5 е1 + 7 е2 + 9 е3)
Или 4 е2 + 16 е3 = (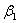 + 5 + 5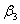 ) е1 + (3 ) е1 + (3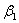 + 2 + 2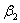 + 7 + 7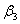 ) е2 + (5 ) е2 + (5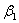 + 9 + 9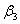 ) е3. ) е3.
Из равенства векторов следует равенство их координат, поэтому получаем систему:
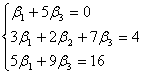
Решая её по формулам Крамера 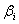 = =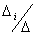 , , 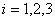 , находим: , находим:
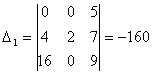 , , 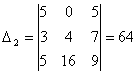 , , 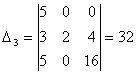 . .
Следовательно, 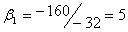 , , 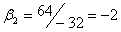 , , 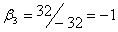 , т.е. координаты вектора , т.е. координаты вектора 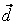 в этом базисе: в этом базисе: 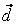 =(1,-1,0). =(1,-1,0).
|







