Решение задачи по высшей математике №438
|
|
Построить на плоскости область решений системы линейных неравенств.
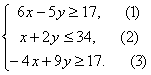
Решение:
Строим область решений системы. Нумеруем ограничения задачи. В прямоугольной декартовой системе координат (см. рис.) строим прямую 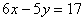 ( (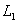 ), соответствующую ограничению (1). Находим, какая из двух полуплоскостей, на которые эта прямая делит всю координатную плоскость, является областью решений неравенства (1). Для этого достаточно координаты какой-либо точки, не лежащей на прямой, подставить в неравенство. Так как прямая ), соответствующую ограничению (1). Находим, какая из двух полуплоскостей, на которые эта прямая делит всю координатную плоскость, является областью решений неравенства (1). Для этого достаточно координаты какой-либо точки, не лежащей на прямой, подставить в неравенство. Так как прямая 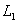 не проходит через начало координат, подставляем координаты точки О (0, 0) в первое ограничение 0 + 0 ? 17. Получаем неравенство 0 ? 17. Следовательно, точка О не лежит в полуплоскости решений. Таким образом, стрелки на концах прямой не проходит через начало координат, подставляем координаты точки О (0, 0) в первое ограничение 0 + 0 ? 17. Получаем неравенство 0 ? 17. Следовательно, точка О не лежит в полуплоскости решений. Таким образом, стрелки на концах прямой 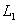 должны быть направлены в полуплоскость, не содержащую точку О. Аналогично строим прямые должны быть направлены в полуплоскость, не содержащую точку О. Аналогично строим прямые 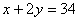 ( (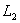 ), ), 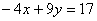 ( (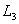 ), и области решений ограничений (2) и (3). Находим общую часть полуплоскостей решений; полученную область допустимых решений отметим (см. рис.) штриховкой. ), и области решений ограничений (2) и (3). Находим общую часть полуплоскостей решений; полученную область допустимых решений отметим (см. рис.) штриховкой.
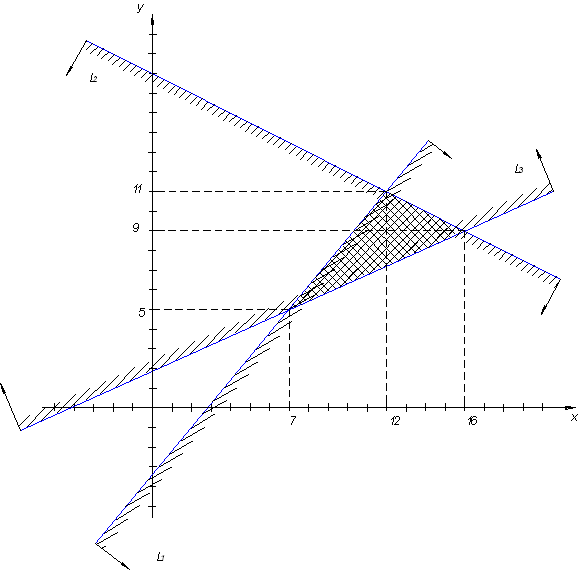
Найдем теоретически точки пересечений прямых:
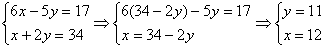
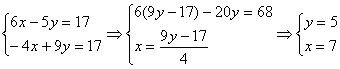
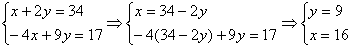
|







