Доказать совместность данной системы линейных уравнений и решить ее двумя способами: 1) методом Гаусса;  2) средствами матричного исчисления.

Решение:
 Запишем матрицу коэффициентов системы А и расширенную матрицу системы В: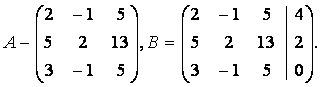  
Вертикальной чертой мы отделили элементы матрицы системы  от свободных членов системы. Определим ранги матрицы А и В.
Для этого проведём преобразования матрицы В:

1. Отнимем от элементов второй строки элементы третьей строки,
2. Первую строку умножим на (-1) и прибавим третью строку;
3. Вторую строку сложим с первой строкой, умноженной на (-2);

Третью строку сложим с первой строкой, умноженной на (-3);

1. Третью строку умножаем на 3, прибавляем к ней вторую.

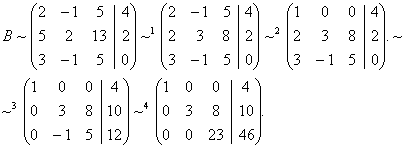
Отсюда следует, что r(В)=3, минор третьего порядка матрицы А

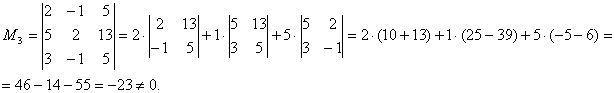
Следовательно, r(B) = r(A) = 3, т.е. данная система совместна.
Но последняя преобразованная матрица В 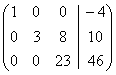- это расширенная матрица системы
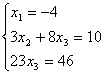
"Обратным ходом" метода Гаусса из последнего уравнения системы находим х3 = 2; из второго х2 = – 2; из первого х1 = – 4
Ответ: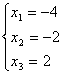  

2) Решение матричным методом:
Прежде всего, найдем матрицу А-1, обратную матрице А.
Определитель основной матрицы системы:
.
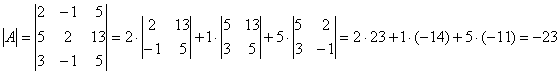Алгебраические дополнения всех элементов:

Отсюда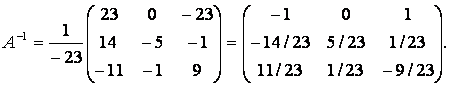
Тогда
Х = = ,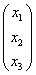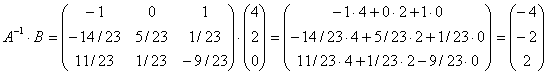

 и, следовательно х1=-4; х2=-2; х3=2.