Решение задачи по высшей математике №433
|
|
Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей.

Решение:
- Характеристическое уравнение данного преобразования имеет вид:
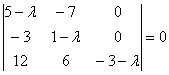
Корни этого уравнения следующие: 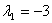 ; ; 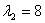 ; ; 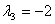
- Все корни являются собственными числами.
- Чтобы найти собственный вектор с собственным числом
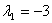 , полагаем в системе , полагаем в системе 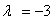 . Получим . Получим
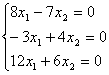
Решение этой системы можно записать в виде
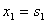 ; ; 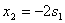 ; ; 
Вектор 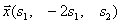 , где , где 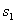 и и 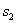 — любые числа, удовлетворяющие условию — любые числа, удовлетворяющие условию 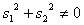 , является собственным вектором данного преобразования с собственным числом , является собственным вектором данного преобразования с собственным числом 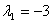 . .
- Аналогично находим собственный вектор с собственным числом
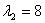 : :
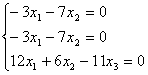
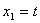 ; ; 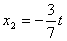 ; ; 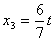
Вектор 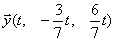 , где , где 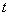 — любое число, удовлетворяющее условию — любое число, удовлетворяющее условию 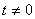 , является собственным вектором данного преобразования с собственным числом , является собственным вектором данного преобразования с собственным числом 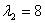 . .
- Аналогично находим собственный вектор с собственным числом
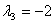 : :
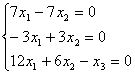
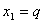 ; ; 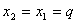 ; ; 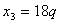
Вектор 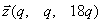 , где , где 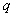 — любое число, удовлетворяющее условию — любое число, удовлетворяющее условию 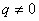 , является собственным вектором данного преобразования с собственным числом , является собственным вектором данного преобразования с собственным числом 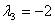 . .
|







