|
Исследовать функцию и построить график у = 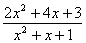 . .
Решение:
1)Область определения функции: х2+х+1?0 ни при каких значениях х, так как
х2+х+1=0
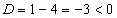
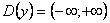
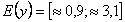 ? См.по графику ? См.по графику
2)Четность, нечетность функции:
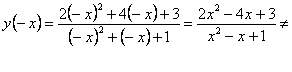
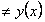 и и 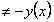 . Следовательно, функция к четным и нечетным не относится. . Следовательно, функция к четным и нечетным не относится.
3)Нули функции и промежутки знакопостоянства.
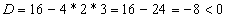 . Действительных корней нет, следовательно, график не пересекает ось ох. . Действительных корней нет, следовательно, график не пересекает ось ох.
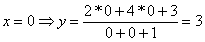
 ? точка пересечения с осью оу. ? точка пересечения с осью оу.
Так как нулей нет, то у>0 при всех действительных значениях х (график располагается выше оси ох).
4)Промежутки возрастания и убывания функции:
Находим производную:
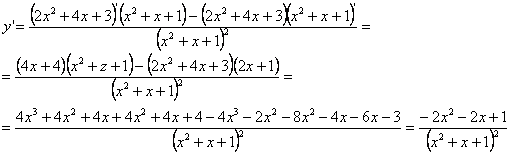

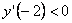 , ,  , , 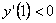 , следовательно на промежутках , следовательно на промежутках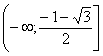 и и 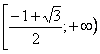 ? функция убывает; на промежутке ? функция убывает; на промежутке 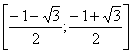 ? функция возрастает. ? функция возрастает.
5)Точки максимума и минимума:
При переходе через точку 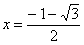 производная меняет знак с «?» на «+», следовательно, производная меняет знак с «?» на «+», следовательно, 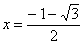 есть точка минимума: есть точка минимума:
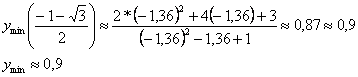
При переходе через точку 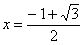 производная меняет знак с «+» на «?», следовательно, производная меняет знак с «+» на «?», следовательно, 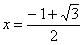 есть точка максимума: есть точка максимума:
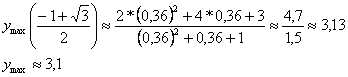
6)Промежутки вогнутости и выпуклости:
Находим:

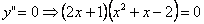
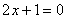 или или 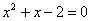
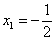 ; ; 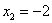 ; ; 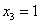 . .
На промежутках 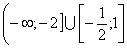 ? выпуклость графика функции направлена вверх (выпукла); ? выпуклость графика функции направлена вверх (выпукла);
На промежутках 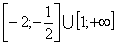 ? выпукла вниз (вогнута). ? выпукла вниз (вогнута).
7)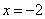 , , 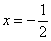 , , 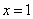 ? точки перегиба, так как ? точки перегиба, так как 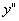 меняет знак при переходе через эти точки. меняет знак при переходе через эти точки.

Точки перегиба: 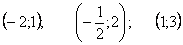
8)Асимптоты:
1)Вертикальных асимптот нет, так как 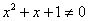
2)Наклонная асимптота 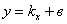 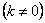
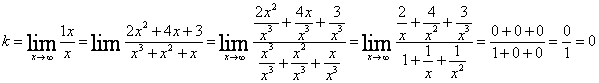
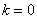 , следовательно, наклонной асимптоты нет. , следовательно, наклонной асимптоты нет.
3)Горизонтальная асимптота:
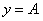 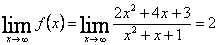 , следовательно, , следовательно, 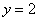 ? горизонтальная асимптота. ? горизонтальная асимптота.
9)Таблица:
х |
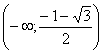
|
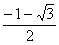
|
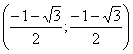
|
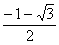
|
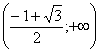
|
у |
+ |
?0,9 |
+ |
?3,1 |
+ |
y' |
+ |
0 |
? |
0 |
+ |
|
|
т.максимума |
|
т.минимума |
|
|
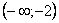
|
?2 |
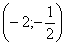
|
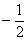
|
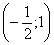
|
1 |
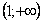
|
y? |
? |
1 |
+ |
2 |
? |
3 |
+ |
|
выпукла
вверх |
точка
перегиба |
выпукла
вниз |
точка
перегиба |
выпукла
вверх |
точка
перегиба |
выпукла
вниз |
|







