|
Даны координаты вершин пирамиды  , ,  , ,  , , 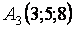 , ,  . Найти: 1) длину ребра . Найти: 1) длину ребра 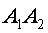 ; 2) угол между ребрами ; 2) угол между ребрами  и и  ; ;
3) угол между ребром 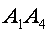 и гранью и гранью  ; 4) площадь грани ; 4) площадь грани  ; ;
5) объем пирамиды ; 6) уравнение прямой  ; 7) уравнение плоскости ; 7) уравнение плоскости  ; 8) уравнение высоты опущенной из вершины ; 8) уравнение высоты опущенной из вершины  на грань на грань 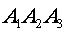 . Сделать чертеж. . Сделать чертеж.
Решение:
- Длину ребра
 найдем как длину вектора найдем как длину вектора  по формуле: по формуле:
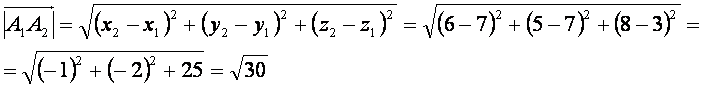
2) Угол между ребрами  и и  найдем как угол между векторами найдем как угол между векторами  и и
 , пользуясь определением скалярного произведения : , пользуясь определением скалярного произведения :


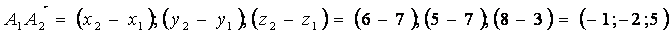
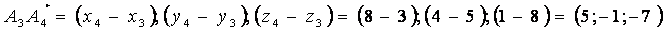

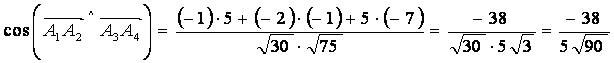
Откуда  = =  ? 143? ? 143?
- Угол между ребром
 и гранью и гранью  найдем по формуле найдем по формуле
 , ,
где  нормальный вектор плоскости нормальный вектор плоскости 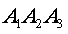
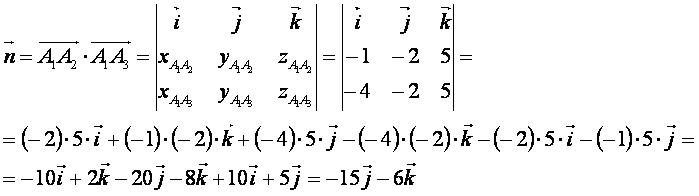 
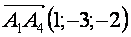

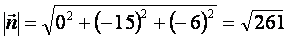
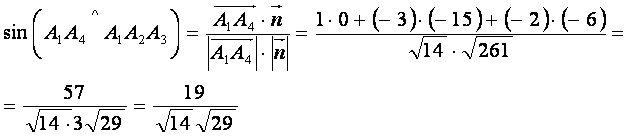
Откуда,  ? 71? ? 71?
- Площадь грани
 вычислим с помощью векторного произведения вычислим с помощью векторного произведения
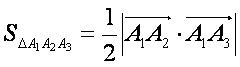
Из предыдущего решения видно, что   , значит , значит
 , отсюда находим , отсюда находим

- Объем пирамиды
 вычислим с помощью смешанного произведения трех векторов, на которых построена пирамида вычислим с помощью смешанного произведения трех векторов, на которых построена пирамида
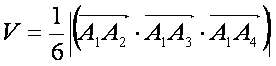
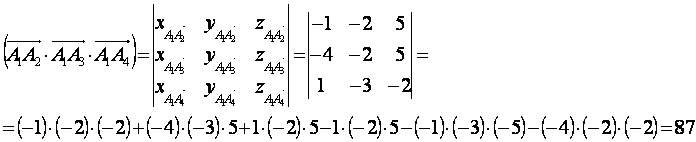
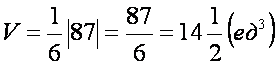
- Уравнение прямой
 найдем по формуле уравнения прямой проходящей через две точки: найдем по формуле уравнения прямой проходящей через две точки:

  , отсюда уравнение имеет вид: , отсюда уравнение имеет вид:
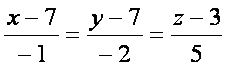
- Для того чтобы составить уравнение плоскости
 , возьмем текущую точку , возьмем текущую точку  плоскости. Векторы плоскости. Векторы  , ,  , ,  лежат в этой плоскости, т.е. они являются компланарными. Воспользуемся условием компланарности трех векторов: лежат в этой плоскости, т.е. они являются компланарными. Воспользуемся условием компланарности трех векторов:
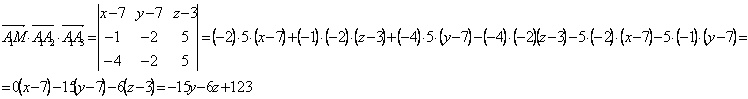
В силу условия компланарности уравнение плоскости  имеет вид: имеет вид:
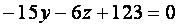
- Чтобы составить уравнение высоты, опущенной из вершины
 на грань на грань 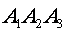 , ,
воспользуемся каноническими уравнениями прямой:
 , где , где  - координаты точки, через которую проходит прямая (в нашем случае это точка - координаты точки, через которую проходит прямая (в нашем случае это точка  ), а ), а  - координаты направляющего вектора - координаты направляющего вектора  . Т.к. прямая и плоскость . Т.к. прямая и плоскость  перпендикулярны, то нормальный вектор плоскости перпендикулярны, то нормальный вектор плоскости 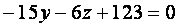 параллелен прямой. Поэтому за направляющий вектор прямой берем вектор параллелен прямой. Поэтому за направляющий вектор прямой берем вектор  , найденный прежде в предыдущем(3) задании. Уравнение прямой, опущенной из вершины , найденный прежде в предыдущем(3) задании. Уравнение прямой, опущенной из вершины  , имеет вид: , имеет вид:

|







