|
Линия задана уравнением  в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от 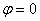 до до 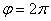 и придавая ? значения через промежуток и придавая ? значения через промежуток 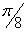 ; 2) найти уравнение данной линии в декартовой системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс с полярной осью; 3) по уравнению в декартовой прямоугольной системе координат определить, какая это линия. ; 2) найти уравнение данной линии в декартовой системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс с полярной осью; 3) по уравнению в декартовой прямоугольной системе координат определить, какая это линия.

Решение:
Для построения линии в полярной системе координат составим таблицу значений полярного радиуса r при определенных значениях полярного угла ?
|
? |
cos? |
6+3cos? |

|
1 |
0 |
1 |
9 |
0,556 |
2 |

|
0,924 |
8,772 |
0,570 |
3 |

|
0,707 |
8,121 |
0,616 |
4 |

|
0,383 |
7,148 |
0,699 |
5 |

|
0,000 |
6,000 |
0,833 |
6 |

|
-0,383 |
4,852 |
1,031 |
7 |

|
-0,707 |
3,879 |
1,289 |
8 |

|
-0,924 |
3,228 |
1,549 |
9 |

|
-1 |
3 |
1,667 |
10 |

|
-0,924 |
3,228 |
1,549 |
11 |

|
-0,707 |
3,879 |
1,289 |
12 |

|
-0,383 |
4,852 |
1,031 |
13 |

|
0,000 |
6,000 |
0,833 |
14 |

|
0,383 |
7,148 |
0,699 |
15 |

|
0,707 |
8,121 |
0,616 |
16 |

|
0,924 |
8,772 |
0,570 |
17 |

|
1 |
9 |
0,556 |
Используя данные таблицы, строим линию:

Для получения уравнения в декартовой системе координат используем формулы перехода от полярной системы координат к декартовой:
 , , 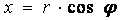 , , 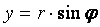 , , 










 


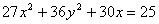
 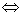 выделим полный квадрат трехчлена выделим полный квадрат трехчлена 





Полученная линия – эллипс.
|







