|
Дано комплексное число 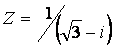 . Требуется: 1) записать число Zв алгебраической и тригонометрической формах; 2) найти все корни уравнения . Требуется: 1) записать число Zв алгебраической и тригонометрической формах; 2) найти все корни уравнения 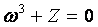 . .
Решение:
Комплексные числа, числа вида Z= a + ib, где a и b — действительные числа, а i — так называемая мнимая единица (число, квадрат которого равен —1); a называют действительной частью, а b — мнимой частью комплексного числа Z. Число z=a-ibназывается сопряженным числу z=a+ib.
Запись комплексного числа в виде a + bi называется алгебраической формой комплексного числа.
С геометрической точки зрения числу Zможно сопоставить вектор, направленный из начала координат в точку Zс координатами aи b. Длина этого вектора называется модулем комплексного числа и определяется равенством


Угол, образованный вектором Zс положительным направлением оси ОХ, называется аргументом числа Zи обозначается Argz. Для аргумента ? справедливы формулы :
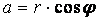 , ,  , , 
Значения Argzопределяются не однозначно, а с точностью до слагаемого 2k?, где k– любое целое число. Таким образом, любое комплексное число z имеет бесконечное множество аргументов, отличающихся друг от друга на число, кратное 2?.
Argz=?+2k?, если k = 0, то мы получим Argz=? - главное значение аргумента .
Если в запись комплексного числа z вместо a и b подставить эти значения
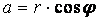 , ,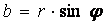 , ,
то получим

Таким образом, мы получили новую форму записи комплексного числа:
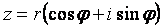 где, r- модуль комплексного числа, ? - главное значение его аргумента. где, r- модуль комплексного числа, ? - главное значение его аргумента.
которая называется тригонометрической формой комплексного числа.
Данное число 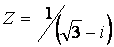 , запишем в алгебраической форме. Для этого умножим числитель и знаменатель на , запишем в алгебраической форме. Для этого умножим числитель и знаменатель на 

Чтобы число  записать в тригонометрической форме, найдем его модуль и главное значение аргумента: записать в тригонометрической форме, найдем его модуль и главное значение аргумента:

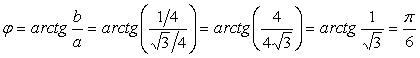

2) Решим уравнение  . .

Представим число 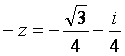 в тригонометрической форме : в тригонометрической форме :

при  , и , и 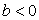 ; при a>0 ; при a<0 и b>0 ; при a>0 ; при a<0 и b>0
 , ,  
В нашем случае  и и 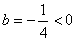 , значит , значит
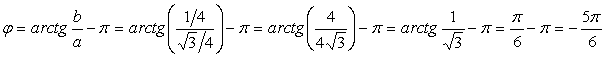 , ,
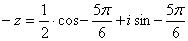
Используем формулу извлечения корня n-ой степени из комплексного числа
 , где k=0,1,2… получим следующее: , где k=0,1,2… получим следующее:
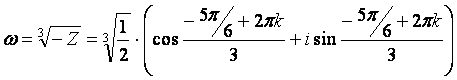 , k = 0,1,2 , k = 0,1,2
Выпишем все значения корня третьей степени.
При k = 0 получим:

При k = 1получим:
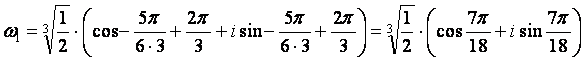
При k = 2получим:
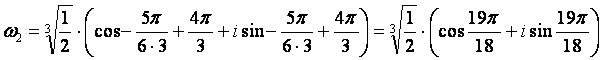
|







