|
Исследовать методами дифференцированного исчисления функцию  , используя результаты исследования, построить ее график. , используя результаты исследования, построить ее график.
Решение:
Исследование функции можно провести по следующей схеме:
Найти область определения функции.
Исследовать на непрерывность, найти точки разрыва графика функции.
Найти уравнения вертикальных, наклонных асимптот, если они существуют.
Выяснить четность, нечетность, периодичность функции.
Найти точки пересечения графика с осями координат.
Найти интервалы монотонности, точки экстремума функции.
Найти интервалы выпуклости, вогнутости графика функции, точки перегиба.
1) Область определения х? . .
2) Данная функция существует всюду, кроме точек  . Точки . Точки 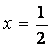 и и  являются точками разрыва. являются точками разрыва.
3) Так как
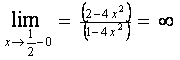 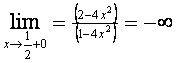
 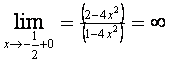
значит прямые,  и и  являются вертикальными асимптотами функции. являются вертикальными асимптотами функции.
Наклонная асимптота имеет уравнение 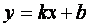 , где , где

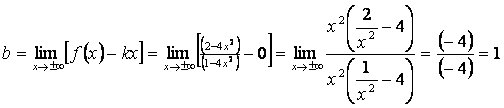
 , ,
значит прямая  является горизонтальной асимптотой функции. является горизонтальной асимптотой функции.
4) Функция является четной, т.к.
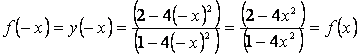
Функция не является периодической.
5) Если х=0, то  , поэтому график функции пересекает ось ОУ в точке , поэтому график функции пересекает ось ОУ в точке
О(0;2). Если у=0, то  , откуда , откуда . Потому график функции пересекает ось ОХ в точках ( . Потому график функции пересекает ось ОХ в точках ( ;0) и ( ;0) и (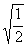 ;0) ;0)
6) Исследуем функцию на экстремум. Точками экстремума могут быть точки, в которых  либо либо 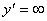
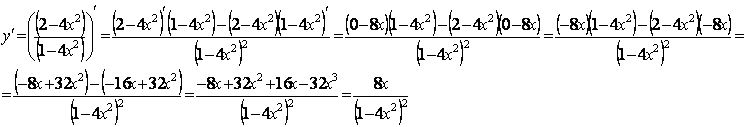
 , при х=0; , при х=0;  , при , при 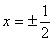
Исследуем критические точки, определяя знак  слева и справа от каждой этой точки. Для сокращения вычислений и для наглядности это исследование удобно записать в виде следующей таблицы: слева и справа от каждой этой точки. Для сокращения вычислений и для наглядности это исследование удобно записать в виде следующей таблицы:
х |
(-?, ) ) |
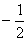
|
( ,0) ,0) |
0 |
(0, ) ) |
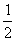
|
( ,?) ,?) |
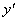
|
- |
? |
- |
0 |
+ |
? |
+ |
y |
убывает |
Нет экстр. |
убывает |
2
min |
возрастает |
Нет экстр. |
возрастает |
Исследуемая функция имеет одну точку экстремума – точку минимума х=0, где  . .
7) Точками перегиба могут быть точки, в которых  либо либо 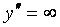
 \ \
 ; ;  при при  и и 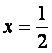
Так как  и и  не принадлежат области определения функции, поэтому точек перегиба нет. не принадлежат области определения функции, поэтому точек перегиба нет.
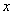
|
(-?,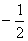 ) ) |
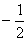
|
(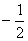  ,) ,) |
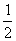
|
( ,?) ,?) |
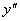
|
- |
? |
+ |
? |
- |

|
вып.вверх |
? |
вып.вниз |
? |
вып.вверх |
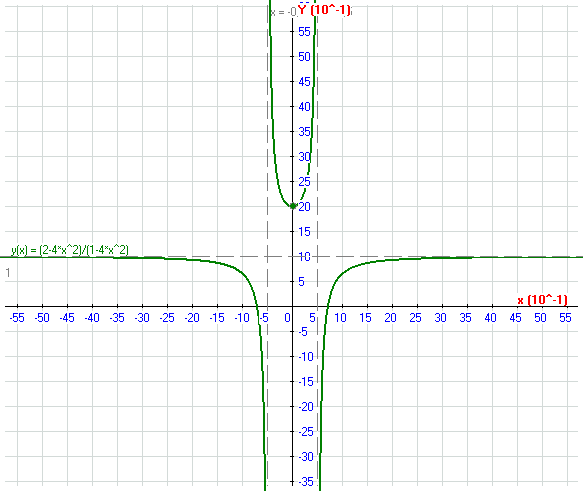
Построим график функции:
|







