Исследовать на экстремум функцию  .
Решение:
Для заданной функци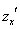и   и  всегда существуют, и для нахождения стационарных (критических) точек запишем систему уравнений:
  ,  или
Решив данную систему, получим х=1, у=4, следовательно, точка М(1;4)является стационарной (критической), в которой может быть экстремум.
Проверим выполнение достаточного условия существования экстремума в этой точке, если значение , то точка М(1;4) будет являться точкой экстремума.

                        

Следовательно, в точке М есть экстремум-минимум,  т.к.