|
Даны векторы 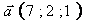 , , 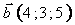 , , 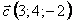 , ,  в некотором базисе. Показать, что в некотором базисе. Показать, что 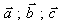 образуют базис и найти координаты вектора образуют базис и найти координаты вектора  в этом базисе. в этом базисе.
Решение :
Равенство 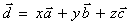 называется разложением вектора называется разложением вектора 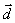 по векторам по векторам  . Нас интересует такие системы векторов, по которым разложение любого вектора пространства возможно и притом единственным образом. Такой системой векторов в пространстве служит любая тройка некомпланарных векторов . Нас интересует такие системы векторов, по которым разложение любого вектора пространства возможно и притом единственным образом. Такой системой векторов в пространстве служит любая тройка некомпланарных векторов 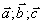 , которые называются базисом пространства, а коэффициенты разложения вектора , которые называются базисом пространства, а коэффициенты разложения вектора 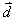 x,y,z– координатами вектора в этом базисе. x,y,z– координатами вектора в этом базисе.
Покажем, что векторы  образуют базис. Смешанное произведение некомпланарных векторов отлично от нуля образуют базис. Смешанное произведение некомпланарных векторов отлично от нуля
 Итак, векторы Итак, векторы  образуют базис. Найдем координаты вектора образуют базис. Найдем координаты вектора 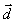 в этом базисе. Равенство в этом базисе. Равенство 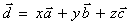 равносильно системе линейных уравнений с тремя неизвестными x, y, z. равносильно системе линейных уравнений с тремя неизвестными x, y, z.

Решим эту систему по правилу Крамера:
 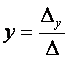 
Вычислим определитель системы линейных уравнений, который составлен из коэффициентов при неизвестных:

Вычислим вспомогательные определители,  которые получаются из определителя системы, путем замены столбца коэффициентов при соответствующей неизвестной, столбцом свободных членов. которые получаются из определителя системы, путем замены столбца коэффициентов при соответствующей неизвестной, столбцом свободных членов.



Решение системы имеет вид:
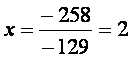  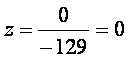
Итак, вектор 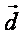 в базисе в базисе 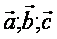 представим в виде представим в виде 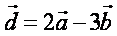 , т.е. имеем координаты ( 2;-3;0 ) . , т.е. имеем координаты ( 2;-3;0 ) .
|







