-
4 |
2 |
0 |
1 |
0 |
2 |
4 |
2 |
0 |
2 |
1 |
1 |
4 |
3 |
1 |
3 |
1 |
2 |
4 |
3 |
4 |
-1 |
2 |
2 |
4 |
3 |
3 |
-2 |
2 |
2 |
Мы рассматриваем парную игру с нулевой суммой, т. е игру двух игроков, где выигрыш первого игрока является проигрышем второго (естественно, возможно наоборот). Данные представлены в виде таблицы, которая называется платежной матрицей. Строки матрицы являются возможными действиями игрока А, столбцы матрицы - возможными действиями игрока В. Возможные действия игроков называются чистыми стратегиями.
В нашем случае, количество чистых стратегий игрока А равно 5 . Количество чистых стратегий игрока В равно 6 .
Допустим, игрок А выберет стратегию A2, а игрок В , в ответ на действие игрока А, выберет стратегию B2. Элемент платежной матрицы 2 расположен на пересечении второго столбца и второй строки платежной матрицы. Другими словами, при выборе игроками данных стратегий , выигрыш игрока А составит 2. Проигрыш игрока В соответственно равен 2. Т.е выигрыш первого игрока равен проигрышу второго. Мы вспомнили, что обозначают коэффициенты платежной матрицы.
Теперь рассмотрим принцип, по которому игроки выбирают свои действия (стратегии). Выбирая стратегию Ai, игрок А должен рассчитывать, что игрок В ответит на нее той из стратегий Bj, для которой выигрыш игрока А минимален (игрок В стремится "навредить" игроку А). Поэтому, последовательно рассмотрим строки платежной матрицы, и в каждой строке выберем наименьший элемент. ( последний столбец в таблице приведенной ниже). Наименьший элемент в каждой строке является наименьшим выигрышем игрока А при любом действии игрока В ( при любой выбранной стратегии игрока В). Естественно, игрок А выберет ту стратегию, при которой он гарантирует себе наибольший выигрыш. Т.е из выбранных наименьших элементов строк платежной матрицы мы выбираем наибольший.
Аналогичные рассуждения могут быть выполнены и в отношении игрока B. Игрок B заинтересован в том, чтобы уменьшить выигрыш игрока А. Выбирая стратегию Bj, он учитывает, что игрок A будет стремиться к максимальному выигрышу. Поэтому последовательно рассмотрим столбцы платежной матрицы и в каждом из них выберем наибольший элемент. Каждый из выбранных элементов показывает наибольший выигрыш игрока А при выборе игроком В данной стратегии. Естественно, игрок В захочет миниминизировать выигрыш игрока А, поэтому из выбранных элементов выберем наименьший.
|
|
Стратегии игрока B |
Минимальный элемент в строке |
B1 |
B2 |
B3 |
B4 |
B5 |
B6 |
Стратегии игрока A |
A1 |
4 |
2 |
0 |
1 |
0 |
2 |
0 |
A2 |
4 |
2 |
0 |
2 |
1 |
1 |
0 |
A3 |
4 |
3 |
1 |
3 |
1 |
2 |
1 |
A4 |
4 |
3 |
4 |
-1 |
2 |
2 |
-1 |
A5 |
4 |
3 |
3 |
-2 |
2 |
2 |
-2 |
Максимальный элемент в столбце |
|
4 |
3 |
4 |
3 |
2 |
2 |
|
Из выбранных наименьших элементов строк платежной матрицы наибольший равен 1 и называется нижней ценой игры. Это гарантированный выигрыш игрока А при любой стратегии игрока В.
Из выбранных элементов столбцов платежной матрицы наименьший равен 2 и называется верхней ценой игры. Это гарантированный минимальный проигрыш игрока В при любой стратегии игрока А.
В нашем случае нижняя цена игры не равна верхней цене игры, т.е игра не имеет решения в чистых стратегиях. (выигрыш игрока А должен равняться проигрышу игрока В, а это у нас не получилось)
В этом случае игра решается в смешанных стратегиях. Смешанный стратегии предполагают, что каждый игрок будет выбирать случайно из возможно допустимых чистых стратегий (но выбирать их с вероятностями), либо частично реализовывать чистые стратегии в заданных пропорциях. Нахождение этих вероятностей (или пропорций) и является решением игры. Таким образом, в общем виде, решением игры являются смешанные стратегии 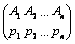 и и 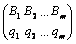 , где , где  и и 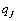 - вероятности чистых стратегий - вероятности чистых стратегий 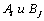 в смешанной. в смешанной.
|
Стратегии игрока B |
B1 |
B2 |
B3 |
B4 |
B5 |
B6 |
A1 |
4 |
2 |
0 |
1 |
0 |
2 |
A2 |
4 |
2 |
0 |
2 |
1 |
1 |
A3 |
4 |
3 |
1 |
3 |
1 |
2 |
A4 |
4 |
3 |
4 |
-1 |
2 |
2 |
A5 |
4 |
3 |
3 |
-2 |
2 |
2 |
Вычеркиваем из таблицы 1-ый столбец, т.к. все его элементы больше или равны элементам 2-го.
Вычеркиваем из таблицы 2-0й столбец, т.к. все его элементы больше или равны элементам 4-му.
Вычеркиваем из таблицы 3-ий столбец, т.к. все его элементы больше или равны элементам 4-го.
Вычеркиваем из таблицы 6-ой столбец, т.к. все его элементы больше или равны элементам 4-го.
Вычеркиваем 1-ю строку, т.к. ее оставшиеся элементы меньше элементов 3-ей.
Вычеркиваем 2-ю строку, т.к. ее оставшиеся элементы меньше элементов 3-ей.
Вычеркиваем 5-ю строку, т.к. ее оставшиеся элементы меньше элементов 4-ой.
В результате получаем матрицу:
|
Стратегии игрока B |
B4 |
B5 |
A3 |
3 |
1 |
A4 |
-1 |
2 |
Решение игры 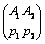 и и 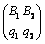 , где , где 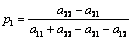 , ,  , , 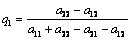 , ,  . Цена игры равна . Цена игры равна 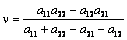 . .
Тогда вероятности чистых стратегий игрока А в смешанной 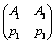 равны: равны:
p3=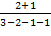 = =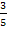 p4= 1- p4= 1-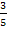 = =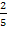
Тогда вероятности чистых стратегий игрока В в смешанной 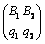 равны: равны:
q 4=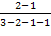 = =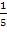 q5= 1- q5= 1-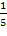 = =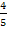
Цена игры равна ? =  = = 
Теперь, мы можем найти оптимальное решение нашей игры.
p*1 = 0, p*2 = 0, p*3 = 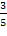 , p*4= , p*4=  , p*5 = 0 , p*6 = 0 . , p*5 = 0 , p*6 = 0 .
q*1 = 0, q*2 = 0, q*3 = 0, q 4=  , q5= , q5= 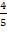 , q*6 = 0 . , q*6 = 0 .
Ответ: P* = ( 0 , 0 , 3/5 , 2/5 , 0 ), Q* = ( 0 , 0 , 0 , 1/5 , 4/5 , 0 ), цена игры v = 7/5
Объяснение ответу: Выигрыш игрока А составит 7/5.
Игрок А: использует стратегию A1 на 0 %, A2 на 0 %, A3 на 60 %, A4 на 40 %, A5 на 0 %
Игрок В: использует стратегию В1 на 0 %, В2 на 0 %, В3 на 0 %, В4 на 20 %, В5 на 80 %, B6 на 0 %
|







