Решение задачи по высшей математике №281
|
|
Знайдіть частинний розв’язок диференціального рівняння, який задовольняє дані початкові умови:
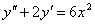

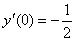
Розв‘язання.
Так як права частина рівняння ?0, маємо неоднорідне рівняння. Загальний розв‘язок неоднорідного рівняння має вигляд:
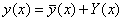 , де , де
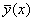 - загальний розв‘язок відповідного однорідного рівняння, - загальний розв‘язок відповідного однорідного рівняння,
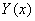 - деякий частинний розв‘язок неоднорідного рівняння. - деякий частинний розв‘язок неоднорідного рівняння.
Спочатку знайдемо загальний розв‘язок відповідного однорідного рівняння.
Характеристичне рівняння відповідного однорідного рівняння:
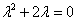
Воно має корені (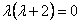 ? ?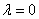 ; ;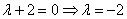 ): ):
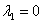 ; ; 
Тому функції 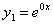 ; ; 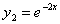 утворюють систему лінійно незалежних розв‘язків диференціального рівняння. утворюють систему лінійно незалежних розв‘язків диференціального рівняння.
Отже загальний розв‘язок однорідного рівняння має вигляд:
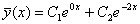
Знайдемо частинний розв‘язок неординарного рівняння методом невизначених коефіцієнтів.
Права частина рівняння має вигляд  (в даному випадку (в даному випадку 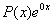 ). Значения ). Значения  є простим коренем характеристичного рівняння. Тоді частинний розв‘язок шукаємо у вигляді є простим коренем характеристичного рівняння. Тоді частинний розв‘язок шукаємо у вигляді 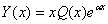 або або 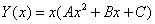 . .
Знайдемо похідні:
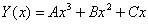
Знайдемо похідні:

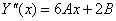
Підставимо значення 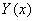 ; ;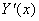 ; ;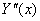 у вихідне рівняння: у вихідне рівняння:
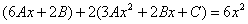 ? ?
?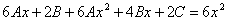 ? ?
?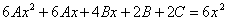 ? ?
?
Прирівнявши коефіцієнти при однакових ступенях ч в обох частинах цієї тотожності, маємо систему рівнянь для знаходження значень А, В, С.
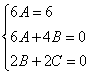
А=1; 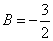 ; ; 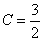 . .
Отже, 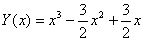 , а загальний розв‘язок неоднорідного рівняння має вигляд: , а загальний розв‘язок неоднорідного рівняння має вигляд:
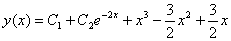
Для знайдення частинного розв‘язання, вирахуємо 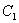 та та 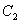 , скориставшись умовами задачі. , скориставшись умовами задачі.
Для цього знайдемо похідну здобутого загального розв‘язку:
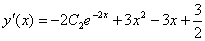
Скористаємося початковими умовами:
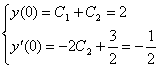 ? ?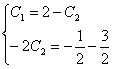 ? ?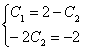 ? ?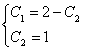
Розв‘язавши систему рівнянь, маємо С1=1; С2=1
Таким чином, шуканий частинний розв’язок диференціального рівняння має вигляд:
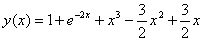
|







