|
Даны векторы 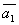 , , 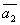 , , 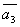 , ,  , ,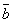 . Доказать, что векторы . Доказать, что векторы 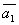 , , 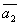 , , 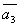 , , 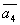 образуют базис четырёхмерного пространства, и найти координаты вектора образуют базис четырёхмерного пространства, и найти координаты вектора 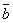 в этом базисе. в этом базисе.
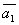 =(2,-1,0,-3) =(2,-1,0,-3)
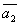 =(-1,1,-2,-1) =(-1,1,-2,-1)
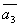 =(0,1,1,-1) =(0,1,1,-1)
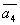 =(1,0,-2,0) =(1,0,-2,0)
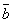 =(0,-1,4,-7) =(0,-1,4,-7)
Решение:
Чтобы векторы образовывали базис, они должны быть линейно независимы. Составим определитель из координат векторов  , ,  , ,  , ,  и вычислим его. Если он не равен нулю, то векторы линейно независимы и, следовательно, образуют базис. и вычислим его. Если он не равен нулю, то векторы линейно независимы и, следовательно, образуют базис.

Т.к. 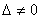 , то векторы , то векторы 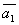 , , 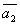 , ,  , , 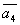 линейно независимы и, следовательно, образуют базис четырёхмерного пространства. линейно независимы и, следовательно, образуют базис четырёхмерного пространства.
Найдем координаты вектора  в этом базисе. Для этого решим систему уравнений методом Гаусса. Приведём систему к «почти треугольному» виду: в этом базисе. Для этого решим систему уравнений методом Гаусса. Приведём систему к «почти треугольному» виду:
 
2 |
-1 |
0 |
1 |
0 |
-1 |
1 |
1 |
0 |
-1 |
0 |
-2 |
1 |
-2 |
4 |
-3 |
-1 |
-1 |
0 |
-7 |
*2
  *2 *2
2 |
-1 |
0 |
1 |
0 |
-2 |
2 |
2 |
0 |
-2 |
0 |
-2 |
1 |
-2 |
4 |
-6 |
-2 |
-2 |
0 |
-14 |
+I
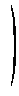 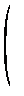 +I*3 +I*3
2 |
-1 |
0 |
1 |
0 |
0 |
1 |
2 |
1 |
-2 |
0 |
-2 |
1 |
-2 |
4 |
 0 0
|
-5 |
-2 |
3 |
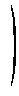 -14 -14
|
+II*2
+II*5
2 |
-1 |
0 |
1 |
0 |
0 |
1 |
2 |
1 |
-2 |
0 |
0 |
5 |
0 |
0 |
0 |
0 |
8 |
8 |
-24 |
Т. к.  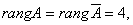 по теореме Кронекера – Капелли система совместна и имеет единственное решение. по теореме Кронекера – Капелли система совместна и имеет единственное решение.
Восстановим систему и решим её снизу – вверх:
 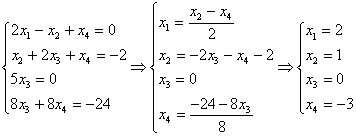
Проверка: 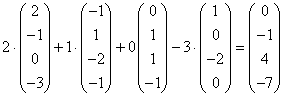 - верно! - верно!
Ответ: вектор  в новом базисе будет выглядеть так: в новом базисе будет выглядеть так: 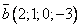
|







