|
Исследовать функцию и построить график:

Решение:
1. Область определения функции:
Т.к. x?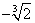 , то , то
D(у): xI(-?; 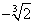 ) E ( ) E (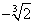 ;+?) ;+?)
2. Четность и нечетность функции:
 , ? данная функция свойствами чётности и нечётности не обладает, и ее график не будет симметричен ни относительно начала координат, ни относительно оси ОУ. , ? данная функция свойствами чётности и нечётности не обладает, и ее график не будет симметричен ни относительно начала координат, ни относительно оси ОУ.
3. Периодичность функции:
Данная функция не является периодической как дробно-рациональная.
4. Непрерывность функции.
Данная функция является непрерывной на всей области определения.
5. Асимптоты графика функции:
а) вертикальные асимптоты:
Т.к. данная функция неопределенна в точке x = : :

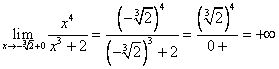
 x = x =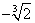 вертикальная асимптота графика. вертикальная асимптота графика.
б) горизонтальные асимптоты:


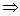 горизонтальных асимптот нет. горизонтальных асимптот нет.
в) наклонные асимптоты:
y=k?x+b
 , ,

? y= x – наклонная асимптота графика.
6. Интервалы монотонности и точки экстремумов:
Найдем производную функции.

Видим, что производная 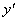 существует при любых значениях х? существует при любых значениях х?
 , ? , ? 
Итак, имеется две критические точки: х1=0 и х2=-2, которые делят область определения функции на интервалы монотонности:
(-?; -2) E (-2; 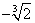 ) E ( ) E (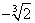 ; 0) E (0;+?) ; 0) E (0;+?)
Составим таблицу для определения знака производной:
x |
(-?; -2) |
-2 |
(-2;  ) ) |
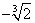
|
( ; 0) ; 0) |
0 |
(0;+?) |
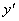
|
+ |
|
- |
|
- |
|
+ |
y |
возрастает |
max
y max
=-8/3 |
убывает |
Разрыв 2ого рода |
убывает |
min
y min =0 |
возрастает |
Итак, точка минимума: В(0; 0)
точка максимума: А(-2; -8/3)
7. Интервалы выпуклости, вогнутости, точки перегиба
Найдем вторую производную

 ? ? 
Итак, существует две точки, подозрительные на перегиб: х1=0 и х2=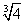 , они делят область определения функции на интервалы: , они делят область определения функции на интервалы:
(-?;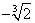 ) E ( ) E (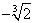 ; 0) E (0; ; 0) E (0; 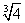 ) E ( ) E (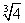 ;+?) ;+?)
Составим таблицу для определения знака второй производной:
x |
(-?; ) ) |
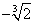
|
( ; 0) ; 0) |
0 |
(0; 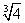 ) ) |

|
(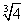 ;+?) ;+?) |
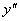
|
- |
|
+ |
|
+ |
перегиб |
- |
y |
выпукла |
|
вогнута |
|
вогнута |
уперегиба=  1,06 1,06 |
выпукла |
Итак, точка перегиба: С(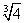 ; ;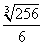 ). ).
8. Точки пересечения графика с осями координат
С осью OY: полагаем x=0, тогда y=0? (.)О(0;0).
С осью OX: полагаем y=0, тогда x=1 ?(.)О(0;0).
9. Дополнительные точки.
x=-7: y=-7
x=4: y=3,92
Построим график функции

|







