|
Даны выборочные варианты х1 и соответствующие им частоты ni количественного признака Х. а) найти выборочные среднюю дисперсию и среднеквадратическое отклонение. б) Считая, что количественный признак Х распределен по нормальному закону и что выборочная дисперсия равна генеральной дисперсии, найти доверительный интервал для оценки математического ожидания с надежностью ?=0,99
хi |
10,2 |
15,2 |
20,2 |
25,2 |
30,2 |
35,2 |
40,2 |
ni |
3 |
15 |
26 |
54 |
12 |
5 |
3 |
Решение
1. Объем выборки
n=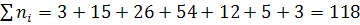
Средняя выборочная:
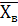 = =
Выборочная дисперсия:
Dв=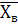 2 – 2 – 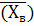 2, где 2, где 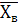 =23,76 =23,76
Средняя выборочная квадратов значений признака ?
 = =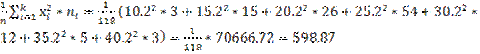
Тогда Dв=598,87-(23,76)2=34,33
Среднее квадратичное отклонение:
?в= ?в= ?в= 5,86 5,86
пусть количественный признак Х генеральной совокупности распределен по нормальному закону, причем среднеквадратическое значение отклонение «?» этого распределения известно. Тогда с вероятностью ? доверительный интервал заданный формулой
 ; ; 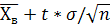 ), ),
покрывает неизвестное математическое ожидание. Здесь число t находится из соотношения 2Ф(t)=? с помощью таблицы интегральной функции Лапласса.
В данной задаче ?=0,99, поэтому 2Ф(t)=0,99, а Ф(t)=0,495, по таблице находим t=2,58.
По условию задачи дисперсия генеральной совокупности D=Dв и, следовательно, ?=?в=5,86. ранее найдены значения n=118, и Хв=23,76. Поэтому можно найти доверительный интервал:

(23,76-1,39; 23,76+1,39)
(22,37; 25,15).
Ответ: Хв=23,76; Dв=34,33; ?в=5,86; а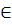 (22,37; 25,15). (22,37; 25,15).
|







