|
По данным корреляционной таблицы найти условные средние Yx и Xy. Оценить тесноту линейной связи между признаками X и Y и составить уравнение линейной регрессии Y по X и X по Y. Сделать чертеж, нанеся на него условные средние и найденные прямые регрессии. Оценить силу связи между признаками с помощью корреляционного отношения.
Y\X |
5 |
10 |
15 |
20 |
25 |
30 |
Ny |
35 |
4 |
2 |
|
|
|
|
6 |
45 |
|
5 |
3 |
|
|
|
8 |
55 |
|
|
5 |
45 |
5 |
|
55 |
65 |
|
|
2 |
8 |
7 |
|
17 |
75 |
|
|
|
4 |
7 |
3 |
14 |
Nx |
4 |
7 |
10 |
57 |
19 |
3 |
n=100 |
Найдем условные средние воспользовавшись формулами:
?x= Xy= Xy=
Yx=5= Xy=35= Xy=35=
Yx=10= Xy=45= Xy=45=
Yx=15= Xy=55= Xy=55=
Yx=20= Xy=65= Xy=65=
Yx=25 Xy=75= Xy=75=
Yx=30
Оценка тесноты линейной связи между признаками X и Y производится с помощью коэффициента линейной корреляции r:

Коэффициент r может принимать значения от -1 до +1.
Знак r указывает на вид связи: прямая или обратная. Абсолютная величина |r| на тесноту связи. При r>0 связь прямая, то есть с ростом х растет у.
При r<0 связь обратная, то есть с ростом х убывает у.
Для нахождения rвычислим указанные общие средние: х, у, ху, а также средние квадратические отклонения ?х и ?у. Вычисления удобно поместить в таблицах, куда вписываем также найденные ранее условные средние.
Значение коэффициента линейной корреляции
Х |
nx |
x*nx |
x2*nx |
 yx yx
|
 x*nx*yx x*nx*yx
|
5 |
4 |
20 |
100 |
35 |
700 |
10 |
7 |
70 |
700 |
42.14 |
2949.8 |
15 |
10 |
150 |
2250 |
54 |
8100 |
20 |
57 |
1140 |
22800 |
57.8 |
65892 |
25 |
19 |
475 |
11875 |
66.05 |
31373.75 |
30 |
3 |
90 |
2700 |
75 |
6750 |
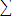
|
100 |
1945 |
40425 |
- |
115765.55 |
Y |
ny |
y*ny |
y2*ny |
 xy xy
|
 y*ny*xy y*ny*xy
|
35 |
6 |
210 |
7350 |
6.67 |
1400.7 |
45 |
8 |
360 |
16200 |
11.875 |
4275 |
55 |
55 |
3025 |
166375 |
20 |
60500 |
65 |
17 |
1105 |
71825 |
21.47 |
23724.35 |
75 |
14 |
1050 |
78750 |
24.64 |
25872 |
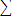
|
100 |
5750 |
340500 |
- |
115772.05 |
С помощью таблиц находим общие средние, средние квадратов, среднюю произведения и среднеквадратические отклонения:
Х=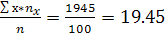
X2=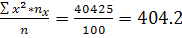 5 5
XY=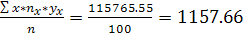
Y=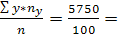 57.5 57.5
Y2=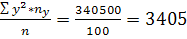
 ?x= ?x=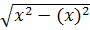 = =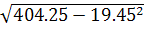 = =
 ?y= ?y= = = =9.94 =9.94
Отсюда коэффициент корреляции равен:
r=
т.к r > 0, то связь прямая, то есть с ростом Х растет Y.
т.к | r | > 0,78 то линейная связь высокая.
Находим линейное уравнение регрессии Y по X:

Yx-57.5=0.78*
Yx=1.52x+27.94
Аналогично находим уравнение регрессии X поY:

Xy-19.45=0.78*
Xy=0.4y-3.55
Данные уравнения устанавливают связь между признаками X и Y и позволяют найти среднее значение признака Yx для каждого значения x и аналогично среднее значение признака Xy для каждого значения y.
Изобразим полученные результаты графически.
  Нанесем на график точки (х;ух) отметив их звездочками( ). Нанесем на график точки (ху;у) отметив их кружочками ( ). Построим каждое из найденных уравнений регрессии по двум точкам: Нанесем на график точки (х;ух) отметив их звездочками( ). Нанесем на график точки (ху;у) отметив их кружочками ( ). Построим каждое из найденных уравнений регрессии по двум точкам:
Yx=1.52x+27.94
 Xy=0.4y-3.55 Xy=0.4y-3.55
Обе прямые регрессии пересекаются в точке (х;у). В нашей задаче это точки (19,45; 57,5).
Оценка тесноты любой связи между признаками производится с помощью корреляционных отношений Y по X и X по Y:
?ух=
Дисперсия 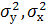 называемые внутригрупповыми, определены ранее. называемые внутригрупповыми, определены ранее.
Величины 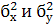 называются межгрупповыми дисперсиями и вычисляются по формулам: называются межгрупповыми дисперсиями и вычисляются по формулам:
    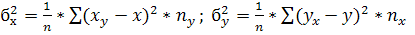
Они характеризуют разброс условных средних, от общей средней. В данной задаче:

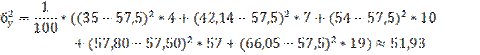
бх=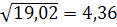
бу=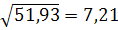
Тогда корреляционные отношения равны:
?ух=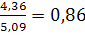
?ху=
Ответ: Корреляционная связь между признаками высокая ее можно описать уравнениями:
Yx=1.52x+27.94,
Xy=0.4y-3.55.
|







