Решение задачи по высшей математике №267
|
- Дослідіть ряд на абсолютну та відносну збіжність:
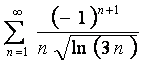
Розв‘язання.
Члени даного ряду спадають за абсолютною величиною:
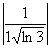 > >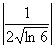 > > > >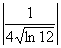 > > >… . >… .
[ 1,05 |
> |
0,67 |
> |
0,49 |
> |
0,39 |
> |
0,33 |
> |
…] |

За ознакою Лейбніца даний ряд збыжний….
Щоб установити, збіжний ряд умовно чи абсолютно, дослідимо ряд із додатними членами
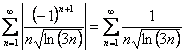
Дослідемо за інтегральною ознакою Коші.
Якщо невласний інтеграл  збігається, то і ряд збіжний. збігається, то і ряд збіжний.

Отже, інтеграл розбіжний. Знаить, ряд із додатними членами теж розбігається.
Відповідь: ряд умовно збіжний.
|







