|
Три стрелки независимо друг от друга сделали по одному выстрелу по мишени. Вероятность попадания для первого стрелка равна 0,9, для второго – 0,8, для третьего – 0,7. Найти закон распределения величины х – числа попадания в мишень. Найти числовые характеристики с.в. Х. Построить функцию распределения.
Решение:
Принимая за случайную величину число попаданий, видим, что она может принимать значения 0, 1, 2, 3. для составления закона распределения этой случайной величины необходимо определить соответствующие вероятности. Примем 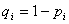
1) Ни один стрелок не промахнулся
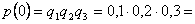 0,006 0,006
2)Один промахнулся
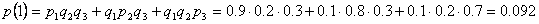
3)Двое промахнулись

4) Все промахнулись
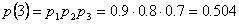
Получаем закон распределения
x |
0 |
1 |
2 |
3 |
p |
0,006 |
0,092 |
0,398 |
0,504 |

Запишем и построим функцию распределения F (x)


Найдем числовые характеристики с.в. Х: математическое ожидание (m), дисперсию (D), среднестатистическое отклонение (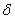 ), моду, коэффициент вариации. ), моду, коэффициент вариации.
Математическое ожидание находится по формуле

Найдем дисперсию по формуле

Случайная величина (Х-М(Х) имеет распределение, представленное в таблице
х-м(х) |
-2,4 |
-1,4 |
-0,4 |
0,6 |
р |
0,006 |
0,092 |
0,398 |
0,504 |
Тогда

Случайная величина 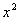 имеет распределение, представленное в таблице имеет распределение, представленное в таблице
0 |
1 |
4 |
9 |
0,006 |
0,092 |
0,398 |
0,504 |
Тогда
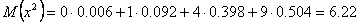
Рассчитаем дисперсию
По формуле 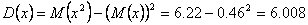
Вычислим среднеквадратическое отклонение по формуле

Мода – наиболее вероятное значение. Из ряда распределения следует, что мода равна 3
Коэффициент вариации находится как отношение среднестатистического отклоненпия к математическому ожиданию.
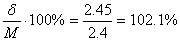
Случайная величина Х задана плотностью вероятностей
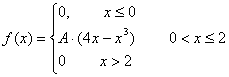
Определить
А)параметр А
Б)функцию распределения F(x)
В)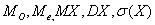
Г)вероятность того, что в трех независимых испытаниях с.в. Х попадет ровно два раза в интервал (-1; 1).
Построить график функции f(X), F(X).
Используя свойство функции плотности распределения вероятностей  найдем коэффициент А найдем коэффициент А
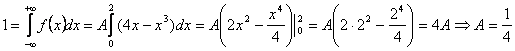
Для нахождения функции распределения вероятностей F(x) воспользуемся формулой
Если  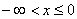 , то , то  , следовательно: , следовательно:

Если 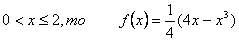 , следовательно: , следовательно:
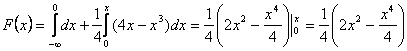
Если 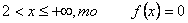 , следовательно: , следовательно:
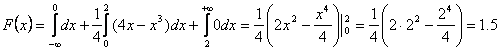
Искомая функция распределения вероятностей есть:
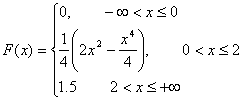
Найдем  (Х) (Х)

Вычислим 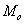 (Х) (Х)
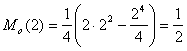
Вычислим математическое ожидание М(Х) случайной величины Х
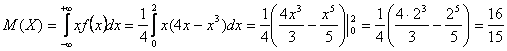
Вычислим дисперсию D(X) случайной величины Х

Найдем среднеквадратическое отклонение 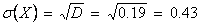
При каждом независимом испытании вероятность попадания в интервал равна
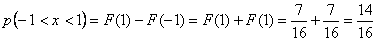
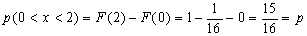
По формуле Бернулли вероятность того что случайная величина в n=3 испытаниях m=2 раза попадет в интервал равна
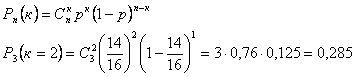
Вероятность равна 28,5%
Построим график функции f(X)

Построить график функции F(X).

|







