Решение задачи по высшей математике №260
|
|
Станок-автомат изготавливает валика, причем контролируется их диаметр Х. Проектный диаметр равен 10 мм и допуск  =00,1 мм. В каком интервале вероятнее всего будут заключены диаметры изготовленных шариков =00,1 мм. В каком интервале вероятнее всего будут заключены диаметры изготовленных шариков
Решение:
1 вариант
Вероятность того, что абсолютная величина отклонения меньше положительного числа  : :
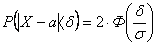 , где , где
Х – непрерывная случайная величина
а – математическое ожидание
 - граница отклонения абсолютной случайной величины - граница отклонения абсолютной случайной величины
Ф – функция Лапласа
 - среднее квадратичное отклонение - среднее квадратичное отклонение
По условию задачи:

Обозначим А – событие «попадание диаметров валика, в который попадают 100% валиков». P(A) = 1. Тогда

Так что интервал по диаметру, в который попадут 100% валиков равен

2 вариант:
Вероятность того, что абсолютная величина отклонения меньше положительного числа  : :
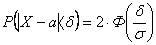
Выполним некоторые числовые расчёты. Если положить  в условии примера 1, то в условии примера 1, то

Последний результат означает, что с вероятностью, близкой к единице (0,9973), случайная величина, подчиняющаяся нормальному закону распределения, не выходит за пределы интервала 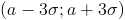 . Это утверждение называют правилом трёх сигм. . Это утверждение называют правилом трёх сигм.

|







