Решение задачи по высшей математике №239
|
|
Дана система линейных дифференциальных уравнений с постоянными коэффициентами
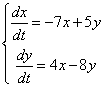 . .
Требуется: 1) найти общее решение системы с помощью характеристического уравнения; 2) записать данную систему и ее решение в матричной форме.
Решение:
1) 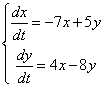
Эту систему можно записать в виде:
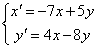
Продифференцируем обе части первого уравнения и исключим из полученного равенства 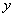 и и 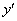 . После дифференцирования получим: . После дифференцирования получим:
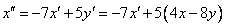
Но из первого уравнения системы следует , что 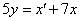 , поэтому , поэтому
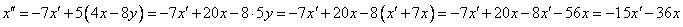
Это уравнение является уравнением второго порядка:
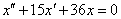
Его характеристическое уравнение
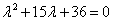 имеет корни имеет корни 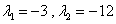
Поэтому общее решение записывается в виде:
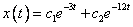
Выражая теперь 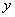 из первого уравнения заданной системы, находим из первого уравнения заданной системы, находим 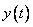 : :
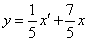

Значит, общее решение системы имеет вид:
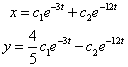
2) 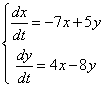
Эту систему можно записать в виде матричного дифференциального уравнения:
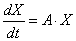
Здесь
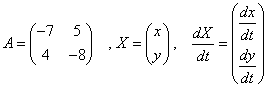
Будем искать частные решения системы в виде
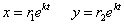 , тогда , тогда
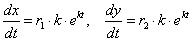
где 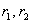 и k - неопределенные коэффициенты, которые следует найти. и k - неопределенные коэффициенты, которые следует найти.
Подставляя эти функции в систему, получим
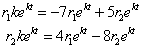
Сокращая на 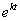 придем к системе линейных однородных алгебраических уравнений относительно придем к системе линейных однородных алгебраических уравнений относительно 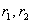
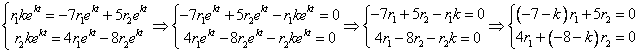
Чтобы эта система однородных уравнений имела ненулевые решения (только такие нас и интересуют), необходимо и достаточно, чтобы ее определитель был равен нулю:
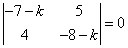
Раскрывая этот определитель, получим характеристическое уравнение:
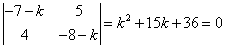
и найдем его корни
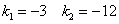
Подставим 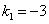 в систему: в систему:

Положим 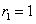 , тогда , тогда 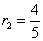
При 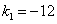
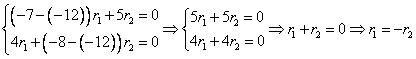
Положим 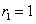 , тогда , тогда 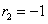
Получаем фундаментальную систему решений:
Для 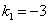 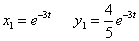
Для 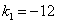 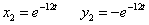
Общее решение системы имеет вид:
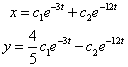
|







