|
Пусть  – координаты произвольного вектора линейного пространства, заданные в некотором базисе. Известен закон изменения координат вектора под действием преобразования – координаты произвольного вектора линейного пространства, заданные в некотором базисе. Известен закон изменения координат вектора под действием преобразования  . .
1. Доказать, что  – линейное преобразование. – линейное преобразование.
2. Составить матрицу линейного преобразования  в том же базисе, в котором заданы координаты вектора в том же базисе, в котором заданы координаты вектора  . .
3. Найти образ вектора 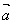 и прообраз вектора и прообраз вектора  под действием преобразования под действием преобразования  . .
4. Найти собственные векторы и собственные значения преобразования 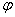 . .
 ; ;  ; ;  . .
Решение.
1) Докажем, что преобразование 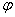 линейное. Рассмотрим векторы линейного пространства линейное. Рассмотрим векторы линейного пространства  и и  , их образы , их образы  , ,  и координатные столбцы этих векторов в том же базисе: и координатные столбцы этих векторов в том же базисе:
 ; ;  ; ;  ; ;  . .
Должно выполняться условие  . .
Вектор  + + имеет столбец координат: имеет столбец координат:
 + + = = . .
Применим преобразование 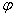 и получим: и получим:
  = = = =
 = = + +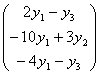 = =  + +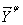 . .
Пусть далее k – произвольное действительное число. Рассмотрим образ вектора k . Координатный столбец . Координатный столбец  при преобразовании при преобразовании 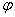 переходит в столбец переходит в столбец
  = =  . .
Таким образом, выполняется и условие  = =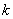  . Доказано, что . Доказано, что  –линейное преобразование. –линейное преобразование.
2) Составим матрицу A , задающую линейное преобразование 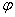 . Из правила умножения матриц следует, что . Из правила умножения матриц следует, что
 = = = = . .
Таким образом, матрица A имеет вид: A= . .
- Найдем образ вектора
 . Для этого умножим матрицу A на столбец его координат: . Для этого умножим матрицу A на столбец его координат:
 = =  = =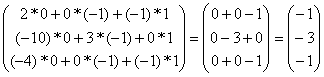 . .
Итак, образ вектора  имеет координаты имеет координаты  . .
Найдем прообраз  вектора вектора  . Пусть вектор . Пусть вектор  имеет координаты имеет координаты 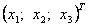 . Тогда . Тогда
  = = ; получаем систему ; получаем систему
Решим систему методом Гаусса.
  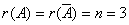 ; ;
Система совместна и имеет единственное решение.
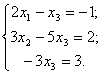


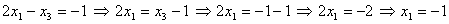
Таким образом, прообраз вектора  имеет координаты имеет координаты  . .
4) Найдём собственные векторы и собственные значения линейного преобразования  . .
A= - матрица линейного преобразования - матрица линейного преобразования 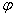 . .
Составим характеристический многочлен:  = =
  . .
Запишем характеристическое уравнение и найдём его корни.
 =0. Тогда, =0. Тогда,  =3; – собственное значение. =3; – собственное значение.
Для собственного значения найдём собственные векторы.
 =3. =3.
 , или , или  Ненулевые решения этой системы являются собственными векторами, принадлежащими собственному значению Ненулевые решения этой системы являются собственными векторами, принадлежащими собственному значению 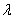 =3. =3.
  
Размерность подпространства решений  решение. решение.
 - свободная переменная; - свободная переменная;  , ,  - зависимые переменные. - зависимые переменные.
Из системы:  =0, =0,  =0. Общее решение: =0. Общее решение:  ; ;  =С; =С; 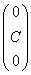 . .
Полагая, С=1, получим собственный вектор  для для 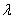 =3. =3.
Ответ: 1)преобразование  - линейное; - линейное;
2) A=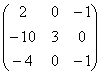 - матрица линейного преобразования - матрица линейного преобразования 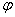 ; ;
3) образ вектора  : :  = =  ; ;
прообраз вектора  : : = = ; ;
4)  =3, =3,  . .
|







