Решение задачи по высшей математике №177
|
|
Исследовать на абсолютную и условную сходимость
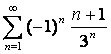 . .
Решение. Проверим выполнение условий теоремы Лейбница
а)  , б) , б) 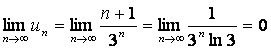
(при вычислении предела применялось правило Лопиталя). Условия выполняются, следовательно, ряд сходится. Исследуем ряд на абсолютную сходимость.
Имеем: 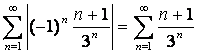 . Тогда по признаку Даламбера: . Тогда по признаку Даламбера:
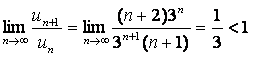 , и ряд, составленный из абсолютных величин элементов исходного ряда, будет сходится. Следовательно, ряд , и ряд, составленный из абсолютных величин элементов исходного ряда, будет сходится. Следовательно, ряд 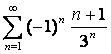 сходится абсолютно. сходится абсолютно.
а) 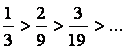 б) б) 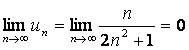 , следовательно ряд , следовательно ряд 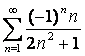 - сходится. - сходится.
2) Пусть 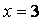 . Тогда . Тогда  . Применим признак сравнения, сравнивая его с расходящимся гармоническим рядом . Применим признак сравнения, сравнивая его с расходящимся гармоническим рядом 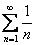 . Имеем . Имеем  . .
Таким образом, ряд 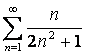 - расходится. - расходится.
Ответ. Область сходимости ряда 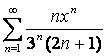 есть интервал есть интервал 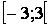 . .
|







