|
Исследуйте функция и постройте ее график.
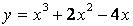 . .
Решение
1. Найдем область определения функции:
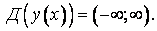
2. Проверим, является ли функция четной или нечетной:
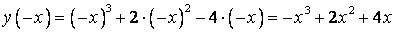 , ,
следовательно, функция не является ни четной, ни нечетной.
3. Найдем точки пересечения графика функции с осями координат.
С осьюОх:  , тогда , тогда 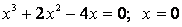 . .
С осью Оу:  , тогда , тогда 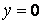 . .
4. Находим первую производную:
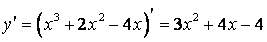
 при при 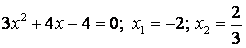 . .
Исследуем знаки производной при переходе через критические точки.

Функция возрастает при . Функция убывает при . Функция убывает при 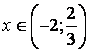 . .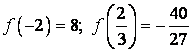 . Получаем . Получаем 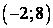 - точка максимума, - точка максимума,  - точка минимума. - точка минимума.
5. Для нахождения интервалов выпуклости и вогнутости и точек перегиба найдем вторую производную:

Вторая производная равна нулю при . .
Наносим на числовую прямую точку  и исследуем знак второй производной на каждом из интервалов. и исследуем знак второй производной на каждом из интервалов.
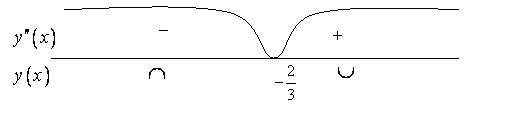

Рис. 1.
В интервале 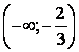 график функции – выпуклый, в интервале график функции – выпуклый, в интервале 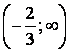 - вогнутый. - вогнутый. 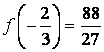 . Получаем . Получаем 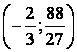 - точка перегиба. - точка перегиба.
6. Находим асимптоты.
Область определения функции – вся числовая прямая, поэтому вертикальных асимптот нет.
Наклонную асимптоту ищем в виде: 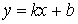 . .

Следовательно, наклонных асимптот нет.
7. Строим график функции (рис. 1):
|







