|
Решить матричное уравнение:
АXBт + m AB = С
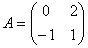 , , 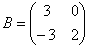 и и 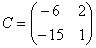 , m=2. , m=2.
Решение.
Для того, чтобы решить заданное матричное уравнение, перенесём все известные слагаемые в правую часть, а неизвестные оставим в левой:

Затем обе части уравнения домножим справа на матрицу, обратную к транспонированной матрице В, и домножим слева на матрицу, обратную к матрице А, получим:
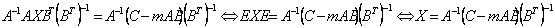
где Е – единичная матрица.
Для того, чтобы найти Х, найдём все необходимые матрицы, затем перемножим их.
 (*) (*)
Запишем транспонированную матрицу Bт, для чего на место столбцов запишем соответствующие строки:
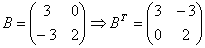
Вычислим произведение матриц А и В, затем умножим полученную матрицу на m=2:

Вычтем полученную матрицу из матрицы С:

Теперь найдём матрицы  . .


Подставляем все найденные матрицы в уравнение (*)

Ответ: 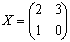 . .
|







