Решение задачи по высшей математике №102
|
- Найдите изолированные особые точки заданной функции
 , выясните их характер и исследуйте поведение функции на бесконечности. , выясните их характер и исследуйте поведение функции на бесконечности.
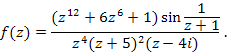
Решение:
Чтобы найти полюса функции , найдём сначала нули функции , найдём сначала нули функции  : :
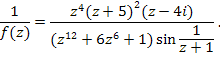
Нулями данной функции будут точки  и и 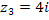 . Порядок указанных нулей функции соответственно четвёртый, второй и первый. Отсюда следует, что функция . Порядок указанных нулей функции соответственно четвёртый, второй и первый. Отсюда следует, что функция 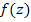 будет иметь в этих точках полюса четвёртого, второго и первого порядков соответственно. будет иметь в этих точках полюса четвёртого, второго и первого порядков соответственно.
Докажем, что точка  является существенно особой. Для этого достаточно взять несколько последовательностей является существенно особой. Для этого достаточно взять несколько последовательностей  , сходящихся к точке , сходящихся к точке  и посмотреть, к какой величине будут сходиться последовательности образов. Например, последовательности и посмотреть, к какой величине будут сходиться последовательности образов. Например, последовательности

сходятся к числу  , в чём нетрудно убедиться. При этом последовательности образов будут сходиться к разным числам. Действительно, выражение , в чём нетрудно убедиться. При этом последовательности образов будут сходиться к разным числам. Действительно, выражение 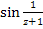 для каждой из указанных последовательностей будет иметь постоянное значение: для каждой из указанных последовательностей будет иметь постоянное значение:



и, соответственно, будет сходиться к разным числам при 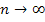 . Поскольку множитель . Поскольку множитель 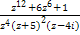 в точке в точке  аналитичен и имеет определённый предел, равный значению этой дроби в данной точке: аналитичен и имеет определённый предел, равный значению этой дроби в данной точке:

то 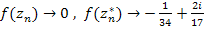 и и 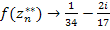 при при 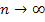 , что явно показывает отсутствие предела функции , что явно показывает отсутствие предела функции  в данной точке. В таком случае точка в данной точке. В таком случае точка 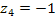 является существенно особой по определению. является существенно особой по определению.
На бесконечности наша функция имеет полюс четвёртого порядка. Действительно, 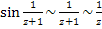 при при  . Тогда . Тогда
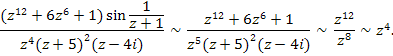
|







