Даны вершины А(х1; у1), В(х2; у2), С(х3, у3) треугольника.
Сделать чертеж и найти:
      1) длину стороны АВ;
 2) внутренний угол А с точностью градуса;
      3) уравнение и длину высоты, опущенной из вершины С;
      4) точку пересечения высот;
      5) уравнение медианы, проведенной через вершину С;
 6) систему линейных неравенств, определяющих треугольник АВС.

Решение:

Сделаем чертёж:

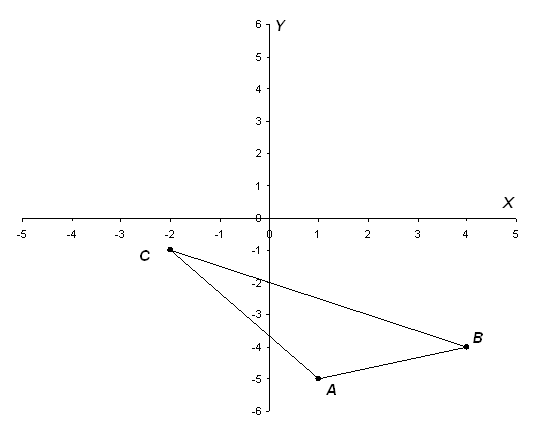
1)длина стороны АВ:  - длина стороны АВ.

2) внутренний угол А с точностью градуса:
Для поиска угла воспользуемся формулой . В данном случае k1=kАB, а k2=kАC - угловые коэффициенты прямых АВ и АС.
Найдем угловые коэффициенты по формуле: .
;                                       ?

? А=arctg(-3)=180°-72°»108° - внутренний угол А.
3) уравнение и длину высоты, опущенной из вершины С:

Составим уравнение высоты CD.
Высота CD перпендикулярна стороне AB. По условию перпендикулярности двух прямых

Составим уравнение высоты CD по известной точке и угловому коэффициенту:
y-yс=k(x-xс)
y+1=-3.(x+2) 
y+1=-3x-6
3x+y+7=0 - уравнение высоты (CD)

Найдем длину высоты CD по формуле для расстояния от точки до прямой:

Составим уравнение прямой AB по угловому коэффициенту и точке A, принадлежащей прямой:
y-yА=kАВ(x-xА)
y+5=(x-1) - Домножим на 3 обе части уравнения:
3y+15=x-1
x-3y-16=0 - уравнение (AB)
Тогда  (ед. дл.) – длина высоты (СD).

4) точку пересечения высот:

Точку пересечения двух прямых можно найти, решив систему уравнений, задающих эти прямые, поэтому нужно найти уравнение еще одной высоты, например, BK.

Составим уравнение высоты (BK) по известной точке и угловому коэффициенту:
y-yВ=k(x-xВ)
y-4=3/4.(x-4) - Домножим на 4 обе части уравнения:
4y-16=3x-12
3x-4y+28=0 - уравнение (BK), тогда
(.) О:     

Таким образом, высоты пересекаются в точке О: (-56/15;63/15)

5) уравнение медианы, проведенной через вершину С:
Найдем координаты точки E как координаты середины отрезка АВ:
                                           

(.)Е: (5/2; -9/2)
Запишем уравнение медианы (CE) по 2 точкам:

-7(x+2)=9(y+1)
-7x-14-9y-9=0
-7x-9y-23=0
7x+9y+23=0 уравнение медианы (CE).

6. Систему линейных неравенств, определяющих треугольник АВС:

 Составим уравнение всех сторон треугольника:
Уравнение стороны АВ уже было составлено: x-3y-16=0

Составим уравнение прямой AС по угловому коэффициенту и точке A, принадлежащей прямой:
y-yА=kАC(x-xА)
y+5=(x-1) - Домножим на 3 обе части уравнения:
3y+15=-4x+4
4x+3y+11=0 - уравнение (АС)

Найдем уравнение стороны (ВС) по 2 точкам:

3.(х-4)=-6.(y+4)
x+2y-4+8=0
x+2y+4=0 - уравнение (BС)

Для определения знаков неравенств в левую часть  каждого уравнения подставим координаты противоположной вершины, которая гарантированно принадлежит соответствующей полуплоскости:
Подставим (.)С (-2;-1) в уравнение (АВ) x-3y-16=-2-3.(-1)-16 =-15<0
Подставим (.)В (4;-4) в уравнение (АС)  4x+3y+11=4.4+3.(-4)+11=15>0
Подставим (.)А (1;-5) в уравнение (ВС)   x+2y+4=1+2. (-5)+4=-5<0

Теперь можно записать систему неравенств:
Ответ:   
1) длина стороны АВ: =
2) внутренний угол А с точностью градуса: А »108°;
3) уравнение и длина высоты, опущенной из вершины С: 3x+y+7=0 - (CD)   иед.дл.
4) точка пересечения высот О: (-56/15;63/15);
5) уравнение медианы, проведенной через вершину С:     7x+9y+23=0 - (CE);
6) система линейных неравенств, определяющих треугольник АВС: